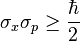Madelung equations

Quantum mechanics
$\sigma_x \sigma_p \ge \frac{\hbar}{2}$ Uncertainty principle
Introduction Glossary History
Background Classical mechanics Old quantum theory Bra–ket notation Hamiltonian Interference
Fundamentals Complementarity Decoherence Entanglement Energy level Measurement Nonlocality Quantum number State Superposition Symmetry Tunnelling Uncertainty Wave function (collapse)
Experiments Afshar Bell's inequality Davisson–Germer Double-slit Elitzur–Vaidman Franck–Hertz Mach–Zehnder Popper Quantum eraser (delayed-choice) Schrödinger's cat Stern–Gerlach Wheeler's delayed-choice
Formulations Overview Heisenberg Interaction Matrix Phase-space Schrödinger Sum-over-histories (path integral)
Equations Dirac Klein–Gordon Pauli Rydberg Schrödinger
Interpretations Overview Bayesian Consistent histories Copenhagen de Broglie–Bohm Ensemble Hidden-variable Many-worlds Objective collapse Quantum logic Relational Stochastic Transactional
Advanced topics Quantum chaos Quantum computing Density matrix Quantum field theory Fractional quantum mechanics Quantum information science Relativistic quantum mechanics Scattering theory Quantum statistical mechanics
Scientists Aharonov Bell Blackett Bloch Bohm Bohr Born Bose de Broglie Candlin Compton Dirac Davisson Debye Ehrenfest Einstein Everett Fock Fermi Feynman Glauber Gutzwiller Heisenberg Hilbert Jordan Kramers Pauli Lamb Landau Laue Moseley Millikan Onnes Planck Rabi Raman Rydberg Schrödinger Sommerfeld von Neumann Weyl Wien Wigner Zeeman Zeilinger

The Madelung equations are Erwin Madelung's equivalent alternative formulation of the Schrödinger equation.

Equations

The Madelung equations^[1] ^[2] are quantum Euler equations:

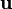\partial_t \rho+\nabla\cdot(\rho\bold u)=0,

\partial_t\bold u+\bold u\cdot\nabla\bold u=-\frac{1}{m}\nabla\left(\frac{1}{\sqrt{\rho}}\hat H\sqrt{\rho}\right)=-\frac{1}{\rho}\nabla\cdot\bold p_Q-\frac{1}{m}\nabla U,

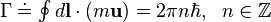where $\bold u$ is the flow velocity in the quantum probability space with mass density $\bold \rho=m|\psi|^2$ . The circulation of the flow velocity field along any closed path obeys the auxiliary condition^[3] $\begin{matrix} \Gamma \doteq \oint{d\mathbf{l}\cdot \left( m\mathbf{u} \right)}=2\pi n\hbar , & n\in \mathbb{Z} \\ \end{matrix}$ . The term in the brackets represents a quantum chemical potential. The kinetic energy operator from the Hamiltonian 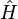$\hat H$ results in a non-local quantum pressure tensor

\bold p_Q=-(\hbar/2m)^2 \rho \nabla\otimes\nabla \ln \rho

or alternatively to the Bohm quantum potential. While the latter is the icon of the de Broglie–Bohm theory, the quantum symbol of the Madelung hydrodynamics is $\bold p_Q$ . The integral energy stored in the quantum pressure tensor is proportional to the Fisher information, which accounts for the quality of measurements. Hence, according to the Cramér–Rao bound, the Heisenberg Uncertainty principle is equivalent to a standard inequality for the efficiency (statistics) of measurements.^[4]

References

↑ Madelung, E. (1926). "Eine anschauliche Deutung der Gleichung von Schrödinger". Naturwissenschaften 14 (45): 1004–1004. Bibcode:1926NW.....14.1004M. doi:10.1007/BF01504657.
↑ Madelung, E. (1927). "Quantentheorie in hydrodynamischer Form". Z. Phys. 40 (3–4): 322–326. Bibcode:1927ZPhy...40..322M. doi:10.1007/BF01400372.
↑ I. Bialynicki-Birula, M. Cieplak, J. Kaminski (1992), Theory of Quanta, Oxford University Press, ISBN 0195071573
↑ Tsekov, R. (2012). "Bohmian Mechanics versus Madelung Quantum Hydrodynamics". doi:10.13140/RG.2.1.3663.8245.

Madelung equations

Equations

See also

References

Further reading