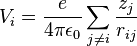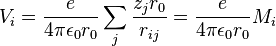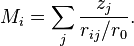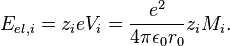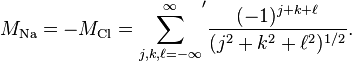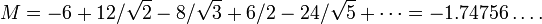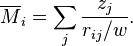Madelung constant

The Madelung constant is used in determining the electrostatic potential of a single ion in a crystal by approximating the ions by point charges. It is named after Erwin Madelung, a German physicist.[1]
Because the anions and cations in an ionic solid are attracting each other by virtue of their opposing charges, separating the ions requires a certain amount of energy. This energy must be given to the system in order to break the anion-cation bonds. The energy required to break these bonds for one mole of an ionic solid under standard conditions is the lattice energy.
Formal expression
The Madelung constant shall allow for the calculation of the electric potential Vi of all ions of the lattice felt by the ion at position ri
where rij =|ri - rj| is the distance between the ith and the jth ion. In addition,
- zj = number of charges of the jth ion
- e = 1.6022×10−19 C
- 4 π ε0 = 1.112×10−10 C²/(J m).
If the distances rij are normalized to the nearest neighbor distance r0 the potential may be written
with 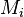 being the (dimensionless) Madelung constant of the ith ion
being the (dimensionless) Madelung constant of the ith ion
The electrostatic energy of the ion at site 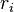 then is the product of its charge with the potential acting at its site
then is the product of its charge with the potential acting at its site
There occur as many Madelung constants 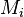 in a crystal structure as ions occupy different lattice sites. For example, for the ionic crystal NaCl, there arise two Madelung constants – one for Na and another for Cl. Since both ions, however, occupy lattice sites of the same symmetry they both are of the same magnitude and differ only by sign. The electrical charge of the Na+ and Cl− ion are assumed to be onefold positive and negative, respectively,
in a crystal structure as ions occupy different lattice sites. For example, for the ionic crystal NaCl, there arise two Madelung constants – one for Na and another for Cl. Since both ions, however, occupy lattice sites of the same symmetry they both are of the same magnitude and differ only by sign. The electrical charge of the Na+ and Cl− ion are assumed to be onefold positive and negative, respectively, 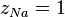 and
and 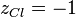 . The nearest neighbour distance amounts to half the lattice parameter of the cubic unit cell
. The nearest neighbour distance amounts to half the lattice parameter of the cubic unit cell 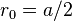 and the Madelung constants become
and the Madelung constants become
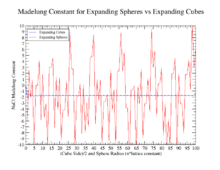
The prime indicates that the term 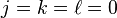 is to be left out. Since this sum is conditionally convergent it is not suitable as definition of Madelung's constant unless the order of summation is also specified. There are two "obvious" methods of summing this series, by expanding cubes or expanding spheres. The latter, though devoid of a meaningful physical interpretation (there are no spherical crystals) is rather popular because of its simplicity. Thus, the following expansion is often found in the literature:[2]
is to be left out. Since this sum is conditionally convergent it is not suitable as definition of Madelung's constant unless the order of summation is also specified. There are two "obvious" methods of summing this series, by expanding cubes or expanding spheres. The latter, though devoid of a meaningful physical interpretation (there are no spherical crystals) is rather popular because of its simplicity. Thus, the following expansion is often found in the literature:[2]
However, this is wrong as this series diverges as was shown by Emersleben in 1951.[3][4] The summation over expanding cubes converges to the correct value. An unambiguous mathematical definition is given by Borwein, Borwein and Taylor by means of analytic continuation of an absolutely convergent series.
There are many practical methods for calculating Madelung's constant using either direct summation (for example, the Evjen method[5]) or integral transforms, which are used in the Ewald method.[6]
| Ion in crystalline compound |  (based on (based on 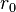 ) ) | 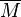 (based on (based on 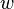 ) ) |
|---|---|---|
| Cl− and Na+ in rocksalt NaCl | ±1.748 | ±3.495 |
| S2− and Zn2+ in sphalerite ZnS | ±1.638 | ±3.783 |
| S− in pyrite FeS2 | … | 1.957 |
| Fe2+ in pyrite FeS2 | … | -7.458 |
Generalization
It is assumed for the calculation of Madelung constants that an ion’s charge density may be approximated by a point charge. This is allowed, if the electron distribution of the ion is spherically symmetric. In particular cases, however, when the ions reside on lattice site of certain crystallographic point groups, the inclusion of higher order moments, i.e. multipole moments of the charge density might be required. It is shown by electrostatics that the interaction between two point charges only accounts for the first term of a general Taylor series describing the interaction between two charge distributions of arbitrary shape. Accordingly, the Madelung constant only represents the monopole-monopole term.
The electrostatic interaction model of ions in solids has thus been extended to a point multipole concept that also includes higher multipole moments like dipoles, quadrupoles etc.[7][8][9] These concepts require the determination of higher order Madelung constants or so-called electrostatic lattice constants. In their case, instead of the nearest neighbor distance 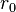 another standard length like the cube root of the unit cell volume
another standard length like the cube root of the unit cell volume ![w=\sqrt[3]{V}](../I/m/207b0848d5c4fe222f564b0910db670b.png) is appropriately used for purposes of normalization. For instance, the Madelung constant then reads
is appropriately used for purposes of normalization. For instance, the Madelung constant then reads
The proper calculation of electrostatic lattice constants has to consider the crystallographic point groups of ionic lattice sites; for instance, dipole moments may only arise on polar lattice sites, i. e. exhibiting a C1, C1h, Cn or Cnv site symmetry (n = 2, 3, 4 or 6).[10] These second order Madelung constants turned out to have significant effects on the lattice energy and other physical properties of heteropolar crystals.[11]
Application to Organic Salts
The Madelung Constant is also a useful quantity in describing the lattice energy of organic salts. Izgorodina and coworkers have described a generalised method (called the EUGEN method) of calculating the Madelung constant for any crystal structure.[12]
References
- ↑ Madelung E (1918). "Das elektrische Feld in Systemen von regelmäßig angeordneten Punktladungen". Phys. Zs. XIX: 524–533.
- ↑ Charles Kittel: Introduction to Solid State Physics., Wiley 1995, ISBN 0-471-11181-3
- ↑ O. Emersleben: Mathematische Nachrichten 4 (1951), 468
- ↑ D. Borwein, J. M. Borwein, K. F. Taylor: "Convergence of Lattice Sums and Madelung's Constant", J. Math. Phys. 26 (1985), 2999–3009, doi:10.1063/1.526675
- ↑ H. M. Evjen: "On the Stability of Certain Heteropolar Crystals", Phys. Rev. 39 (1932), 675–687, http://link.aps.org/abstract/PR/v39/p675
- ↑ P. P. Ewald: "Die Berechnung optischer und elektrostatischer Gitterpotentiale", Ann. Phys. 64 (1921), 253–287, doi:10.1002/andp.19213690304
- ↑ J. Kanamori, T. Moriya, K. Motizuki, and T. Nagamiya (1955). "Methods of Calculating the Crystalline Electric Field". J. Phys. Soc. Jap. 10: 93–102. doi:10.1143/JPSJ.10.93.
- ↑ B. R. A. Nijboer and F. W. de Wette (1957). "On the calculation of lattice sums". Physica 23: 309–321. Bibcode:1957Phy....23..309N. doi:10.1016/S0031-8914(57)92124-9.
- ↑ E. F. Bertaut (1978). "The equivalent charge concept and its application to the electrostatic energy of charges and multipoles". J. Phys. (Paris) 39: 1331–48. Bibcode:1978JPCS...39...97B. doi:10.1016/0022-3697(78)90206-8.
- ↑ M. Birkholz (1995). "Crystal-field induced dipoles in heteropolar crystals – I. concept". Z. Phys. B 96: 325–332. Bibcode:1995ZPhyB..96..325B. doi:10.1007/BF01313054.
- ↑ M. Birkholz (1995). "Crystal-field induced dipoles in heteropolar crystals – II. physical significance". Z. Phys. B 96: 333–340. Bibcode:1995ZPhyB..96..333B. doi:10.1007/BF01313055.
- ↑ E. Izgorodina et al. (2009). "The Madelung Constant of Organic Salts". Crystal Growth & Design 9: 4834–4839. doi:10.1021/cg900656z.
External links
- Glasser, Leslie (2012). "Solid-state energetics and electrostatics: Madelung constants and Madelung energies". Inorg. Chem. 51: 2420–2424. doi:10.1021/ic2023852.
- Sakamoto, Y. (1958). "Madelung constants of simple crystals expressed in terms of Born's basic potentials of 15 figures". J. Chem. Phys 28: 164. Bibcode:1958JChPh..28..164S. doi:10.1063/1.1744060.
- Sakamoto, Y. (1958). "Errata 2: Madelung constants of simple crystals expressed in terms of Born's basic potentials of 15 figures". J. Chem. Phys 28: 1253. Bibcode:1958JChPh..28.1253S. doi:10.1063/1.1744387.
- Zucker, I. J. (1975). "Madelung constants and lattice sums for invariant cubic lattice complexes and certain tetragonal structures". J. Phys. A: Math. Gen. 8 (11): 1734. Bibcode:1975JPhA....8.1734Z. doi:10.1088/0305-4470/8/11/008.
- Zucker, I. J. (1976). "Functional equations for poly-dimensional zeta functions and the evaluation of Madelung constants". J. Phys. A: Math. Gen. 9 (4): 499. Bibcode:1976JPhA....9..499Z. doi:10.1088/0305-4470/9/4/006.
- Weisstein, Eric W., "Madelung Constants", MathWorld.
- (sequence A085469 in OEIS)