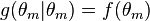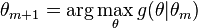MM algorithm

The MM algorithm is an iterative optimization method which exploits the convexity of a function in order to find their maxima or minima. The MM stands for “Majorize-Minimization” or “Minorize-Maximization”, depending on whether you're doing maximization or minimization. MM itself is not an algorithm, but a description of how to construct an optimization algorithm.

The EM algorithm can be treated as a special case of the MM algorithm.[1] However, in the EM algorithm complex conditional expectation and extensive analytical skills are usually involved, while in the MM algorithm convexity and inequalities are our major focus, and it is relatively easier to understand and apply in most of the cases.

History

The original idea of the MM algorithm can be dated back at least to 1970 when Ortega and Rheinboldt were doing their studies related to line search methods.[2] The same idea kept reappearing under different guises in different areas until 2000 when Hunter and Lange put forth "MM" as general frame work.[3] Recently studies have shown that it can be used in a wide range of context, like mathematics, statistics, machine learning, engineering, etc.

How it works

MM algorithm works by finding a surrogate function that minorizes or majorizes the objective function. Optimizing the surrogate functions will drive the objective function upward or downward until a local optimum is reached.

Take the minorize-maximization version for example.

Let 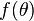f(\theta) be the objective concave function we want to maximize. At the m step of the algorithm, 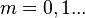m=0,1... , the constructed function 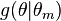g(\theta|\theta_m) will be called the minorized version of the objective function (the surrogate function) at 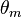\theta_m if

    g(\theta|\theta_m) ≤  f(\theta)   for all  \theta  
    g(\theta_m|\theta_m)=f(\theta_m)

Then we maximize 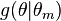g(\theta|\theta_m) instead of 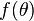f(\theta) , and let

    \theta_{m+1}=\arg\max_{\theta}g(\theta|\theta_m)

The above iterative method will guarantee that 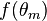f(\theta_m) will converge to a local optimum or a saddle point as m goes to infinity.[4] By the construction we have 

   f(\theta_{m+1}) ≥  g(\theta_{m+1}|\theta_m) ≥  g(\theta_m|\theta_m)= f(\theta_m)

The marching of 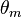\theta_m and the surrogate functions relative to the objective function is shown on the Figure

MM algorithm

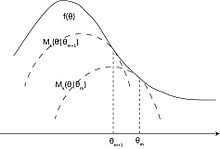
We can just flip the image upside down, and that would be the methodology while we are doing Majorize-Minimization.

Ways to construct surrogate functions

Basically, we can use any inequalities to construct the desired majorized/minorized version of the objective function, but there are several typical choices

References

  1. ↑ Lange, Kenneth. "The MM Algorithm".
  2. ↑ Ortega, J.M.; Rheinboldt, W.C. (1970). "Iterative Solutions of Nonlinear Equations in Several Variables". New York: Academic: 253–255.
  3. ↑ Hunter, D.R.; Lange, K. (2000). "Quantile Regression via an MM Algorithm". Journal of Computational and Graphical Statistics 9: 60–77. doi:10.2307/1390613.
  4. ↑ Wu, C. F. Jeff (Mar 1983). "On the Convergence Properties of the EM Algorithm"