Lyman-alpha line

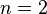In physics, the Lyman-alpha line, sometimes written as Ly- line, is a spectral line of hydrogen, or more generally of one-electron ions, in the Lyman series, emitted when the electron falls from the orbital to the 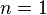orbital, where n is the principal quantum number. In hydrogen, its wavelength of 1215.67 angstroms (121.567 nm or 1.21567 × 10⁻⁷ m), corresponding to a frequency of 2.47 × 10¹⁵ hertz, places the Lyman-alpha line in the vacuum ultraviolet part of the electromagnetic spectrum. Lyman-alpha astronomy must therefore ordinarily be carried out by satellite-borne instruments, except for extremely distant sources whose red-shifts allow the hydrogen line to penetrate the atmosphere.

Because of fine structure perturbations, the Lyman-alpha line splits into a doublet with wavelengths 1215.668 and 1215.674 angstroms. Specifically, because of the electron's spin-orbit interaction, the stationary eigenstates of the perturbed Hamiltonian must be labeled by the total angular momentum j of the electron (spin plus orbital), not just the orbital angular momentum 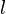. In the 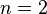orbital, there are two possible states, and 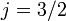, resulting in a spectral doublet. The 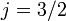state is of higher energy (less negative) and so is energetically farther from the 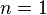orbital to which it is transitioning. Thus, the 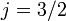state is associated with the more energetic (shorter wavelength) spectral line in the doublet.^[1]

A K-alpha line, or K_α, analogous to the Lyman-alpha line for hydrogen, occurs in the high-energy induced emission spectra of all chemical elements, since it results from the same electron transition as in hydrogen. The equation for the frequency of this line (usually in the X-ray range for heavier elements) uses the same base-frequency as Lyman-alpha, but multiplied by a (Z−1)² factor to account for the differing atomic numbers (Z) of heavier elements, as expressed in Moseley's law. The Lyman-alpha line is most simply described by the {n,m} = {1,2...} solutions to the empirical Rydberg formula for hydrogen's Lyman spectral series. (The Lyman-alpha frequency is produced by multiplying the Rydberg frequency for the atomic mass of hydrogen, R_M (see Rydberg constant), by a factor of 1/1² - 1/2² = 3/4.) Empirically, the Rydberg equation is in turn modeled by the semi-classical Bohr model of the atom.

See also

References