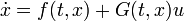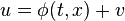Lyapunov redesign

In nonlinear control, the technique of Lyapunov redesign refers to the design where a stabilizing state feedback controller can be constructed with knowledge of the Lyapunov function $V$ . Consider the system

\dot{x} = f(t,x)+G(t,x)[u+\delta(t, x, u)]

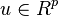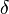where $x \in R^n$ is the state vector and $u \in R^p$ is the vector of inputs. The functions $f$ , $G$ , and $\delta$ are defined for 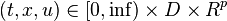$(t, x, u) \in [0, \inf) \times D \times R^p$ , where 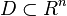$D \subset R^n$ is a domain that contains the origin. A nominal model for this system can be written as

\dot{x} = f(t,x)+G(t,x)u

and the control law

u = \phi(t, x)+v

stabilizes the system. The design of 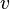$v$ is called Lyapunov redesign.

Lyapunov redesign

Further reading

References