Luttinger parameter

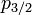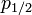In semiconductors, valence bands are well characterized by 3 Luttinger parameters. At the Г-point in the band structure, $p_{3/2}$ and $p_{1/2}$ orbitals form valence bands. But spin-orbit coupling splits sixfold degeneracy into high energy 4-fold and lower energy 2-fold bands. Again 4-fold degeneracy is lifted into heavy- and light hole bands by phenomenological Hamiltonian by J. M. Luttinger.

Three valence band state

In the presence of spin-orbit interaction, total angular momentum should take part in. From the three valence band, l=1 and s=1/2 state generate six state of |j,m_j> as 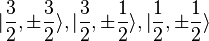$|{3 \over 2}, \pm {3 \over 2} \rangle, |{3 \over 2}, \pm {1 \over 2}\rangle, |{1 \over 2}, \pm {1 \over 2}\rangle$

The spin-orbit interaction from the relativistic quantum mechanics, lowers the energy of j=1/2 states down.

Phenomenological Hamiltonian for the j=3/2 states

Phenomenological Hamiltonian in spherical approximation is written as^[1]

$H= {{\hbar^2} \over {2m_0}} [(\gamma _1+{{5} \over {2}} \gamma _2) \mathbf{k}^2 -2\gamma_2 (\mathbf{k} \cdot \mathbf{J})^2]$

Phenomenological Luttinger parameters $\gamma _i$ are defined as

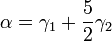
$\alpha = \gamma _1 + {5 \over 2} \gamma _2$

and

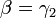
$\beta = \gamma _2$

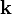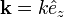If we take $\mathbf{k}$ as $\mathbf{k}=k \hat{e}_z$ , the Hamiltonian is diagonalized for j=3/2 states.

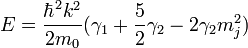
$E = { {\hbar^2 k^2} \over {2m_0} }( \gamma _1 + {{5} \over {2}} \gamma _2 - 2 \gamma _2 m_j^2)$

Two degenerated resulting eigenenergies are

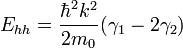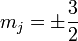
$E _{hh} = { {\hbar^2 k^2} \over {2m_0} }( \gamma _1 - 2 \gamma _2)$ for $m_j = \pm {3 \over 2}$

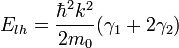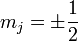
$E _{lh} = { {\hbar^2 k^2} \over {2m_0} }( \gamma _1 + 2 \gamma _2)$ for $m_j = \pm {1 \over 2}$

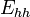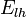$E_{hh}$ ( $E_{lh}$ ) indicates heav-(light-) hole band energy. If we regard the electrons as nearly free electrons, the Luttinger parameters describe effective mass of electron in each bands.

Measurement of Luttinger parameters

Luttinger parameter can be measured by Hot-electron luminescence experiment.

Example: GaAs

$\epsilon _{h,l} = - {{1} \over {2}} \gamma _{1} k^{2} \pm [ {\gamma_{2}}^{2} k^{4} + 3 ({\gamma _{3}}^{2} - {\gamma _{2}}^{2} ) \times ( {k_{x}}^{2} {k_{z}}^{2} + {k_{x}}^{2} {k_{y}}^{2} + {k_{y}}^{2}{k_{z}}^{2})]^{1/2}$

References