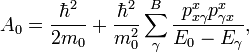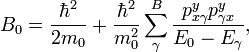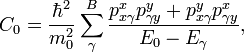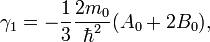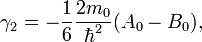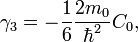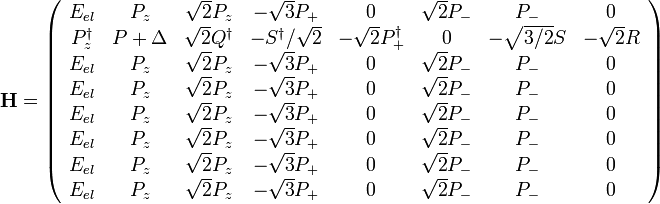Luttinger–Kohn model
A flavor of the k·p perturbation theory used for calculating the structure of multiple, degenerate electronic bands in bulk and quantum well semiconductors. The method is a generalization of the single band k.p theory.
In this model the influence of all other bands is taken into account by using Löwdin's perturbation method.[1]
Background
All bands can be subdivided into two classes (Figure 1):
- Class A: six valence bands (heavy hole, light hole, split off band and their spin counterparts) and two conduction bands.
- Class B: all other bands.
The method concentrates on the bands in Class A, and takes into account Class B bands perturbatively.
We can write the perturbed solution 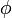 as a linear combination of the unperturbed eigenstates
as a linear combination of the unperturbed eigenstates 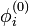 :
:
Assuming the unperturbed eigenstates are orthonormalized, the eigenequation are:
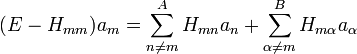 ,
,
where
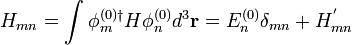 .
.
From this expression we can write:
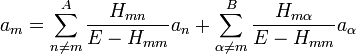 ,
,
where the first sum on the right-hand side is over the states in class A only, while the second sum is over the states on class B. Since we are interested in the coefficients 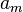 for m in class A, we may eliminate those in class B by an iteration procedure to obtain:
for m in class A, we may eliminate those in class B by an iteration procedure to obtain:
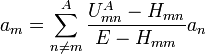 ,
,
Equivalently, for 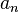 (
(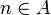 ):
):
and
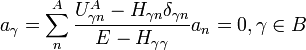 .
.
When the coefficients 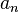 belonging to Class A are determined so are
belonging to Class A are determined so are 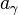 .
.
Schrödinger equation and basis functions
The Hamiltonian including the spin-orbit interaction can be written as:
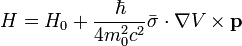 ,
,
where 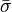 is the Pauli spin matrix vector. Substituting into the Schrödinger equation we obtain
is the Pauli spin matrix vector. Substituting into the Schrödinger equation we obtain
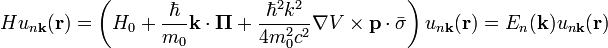 ,
,
where
and the perturbation Hamiltonian can be defined as
The unperturbed Hamiltonian refers to the band-edge spin-orbit system (for k=0). At the band edge, conduction band Bloch waves exhibit s-like symmetry, whole valence band states are p-like (3-fold degenerate without spin). Let us denote these states as 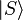 , and
, and 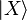 ,
, 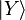 and
and 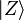 respectively. These Bloch functions can be pictured as periodic repetition of atomic orbitals, repeated at intervals correcsponding to the lattice spacing. The Bloch function can be expanded in the following manner
respectively. These Bloch functions can be pictured as periodic repetition of atomic orbitals, repeated at intervals correcsponding to the lattice spacing. The Bloch function can be expanded in the following manner
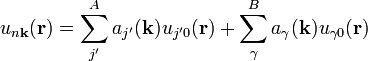 ,
,
where j' is in Class A and 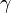 is in Class B. The basis functions can be chosen to be
is in Class B. The basis functions can be chosen to be
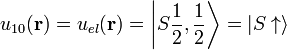
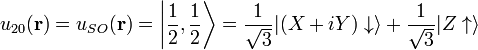
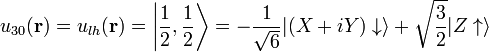
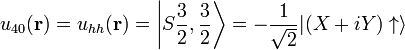
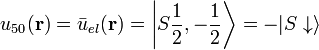
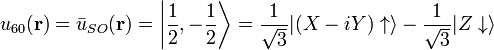
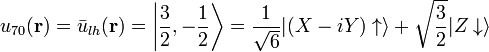
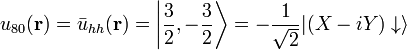 .
.
Using Löwdin's method, only the following eigenvalue problem needs to be solved
where
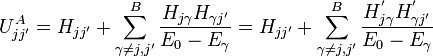 ,
,
The second term of 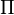 can be neglected compared to the similar term with p instead of k. Similarly to the single band case, we can write for
can be neglected compared to the similar term with p instead of k. Similarly to the single band case, we can write for 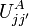
We now define the following parameters
and the band structure parameters (or the Luttinger parameters) can be defined to be
These parameters are very closely related to the effective masses of the holes in various valence bands. 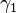 and
and 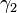 describe the coupling of the
describe the coupling of the 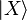 ,
, 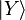 and
and 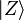 states to the other states. The third parameter
states to the other states. The third parameter 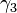 relates to the anisotropy of the energy band structure around the
relates to the anisotropy of the energy band structure around the 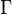 point when
point when 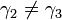 .
.
Explicit Hamiltonian matrix
The Luttinger-Kohn Hamiltonian 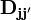 can be written explicitly as a 8X8 matrix (taking into account 8 bands - 2 conduction, 2 heavy-holes, 2 light-holes and 2 split-off)
can be written explicitly as a 8X8 matrix (taking into account 8 bands - 2 conduction, 2 heavy-holes, 2 light-holes and 2 split-off)
References
- ↑ S.L. Chuang (1995). Physics of Optoelectronic Devices (First ed.). New York: Wiley. pp. 124–190. ISBN 0-471-10939-8.
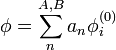
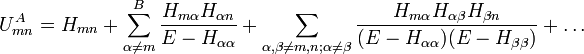
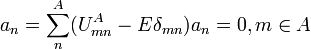
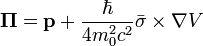
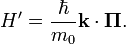
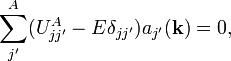
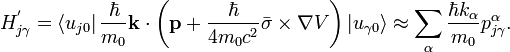
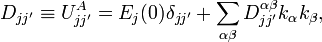
![D^{\alpha\beta}_{jj'} = \frac{\hbar^2}{2 m_0} \left [ \delta_{jj'}\delta_{\alpha\beta} + \sum^{B}_{\gamma} \frac{ p^{\alpha}_{j\gamma}p^{\beta}_{\gamma j'} + p^{\beta}_{j\gamma}p^{\alpha}_{\gamma j'} }{ m_0 (E_0-E_{\gamma}) } \right ].](../I/m/4a7b6b6ebf76729f597fd8fc0b243f0f.png)