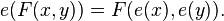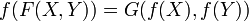Lubin–Tate formal group law
In mathematics, the Lubin–Tate formal group law is a formal group law introduced by Lubin and Tate (1965) to isolate the local field part of the classical theory of complex multiplication of elliptic functions. In particular it can be used to construct the totally ramified abelian extensions of a local field. It does this by considering the (formal) endomorphisms of the formal group, emulating the way in which elliptic curves with extra endomorphisms are used to give abelian extensions of global fields
Definition of formal groups
Let Zp be the ring of p-adic integers. The Lubin–Tate formal group law is the unique (1-dimensional) formal group law F such that e(x) = px + xp is an endomorphism of F, in other words
More generally, the choice for e may be any power series such that
- e(x) = px + higher-degree terms and
- e(x) = xp mod p.
All such group laws, for different choices of e satisfying these conditions, are strictly isomorphic.[1] We choose these conditions so as to ensure that they reduce modulo the maximal ideal to Frobenius and the derivative at the origin is the prime element.
For each element a in Zp there is a unique endomorphism f of the Lubin–Tate formal group law such that f(x) = ax + higher-degree terms. This gives an action of the ring Zp on the Lubin–Tate formal group law.
There is a similar construction with Zp replaced by any complete discrete valuation ring with finite residue class field, where p is replaced by a choice of uniformizer.[2]
Example
We outline here a formal group equivalent of the Frobenius element, which is of great importance in class field theory,[3] generating the maximal unramified extension as the image of the reciprocity map.
For this example we need the notion of an endomorphism of formal groups, which is a formal group homomorphism f where the domain is the codomain. A formal group homomorphism from a formal group F to a formal group G is a power series over the same ring as the formal groups which has zero constant term and is such that:
Consider a formal group F(X,Y) with coefficients in the ring of integers in a local field (for example Zp), taking X and Y to be in the unique maximal ideal gives us a convergent power series and in this case we define F(X,Y) = X +F Y and we have a genuine group law. For example if F(X,Y)=X+Y, then this is the usual addition. This is isomorphic to the case of F(X,Y)=X+Y+XY, where we have multiplication on the set of elements which can be written as 1 added to an element of the prime ideal. In the latter case f(S) = (I + S)p-1 is an endomorphism of F and the isomorphism identifies f with the Frobenius element.
Generating ramified extensions
Lubin–Tate theory is important in explicit local class field theory. The unramified part of any abelian extension is easily constructed, Lubin–Tate finds its value in producing the ramified part. This works by defining a family of modules (indexed by the natural numbers) over the ring of integers consisting of what can be considered as roots of the power series repeatedly composed with itself. The compositum of all fields formed by adjoining such modules to the original field gives the ramified part.
A Lubin–Tate extension of a local field K is an abelian extension of K obtained by considering the p-division points of a Lubin–Tate group. If g is an Eisenstein polynomial, f(t) = t g(t) and F the Lubin–Tate formal group, let θn denote a root of gfn-1(t)=g(f(f(⋯(f(t))⋯))). Then K(θn) is an abelian extension of K with Galois group isomorphic to U/1+pn where U is the unit group of the ring of integers of K and p is the maximal ideal.[2]
Connection with stable homotopy theory
Lubin and Tate studied the deformation theory of such formal groups. A later application of the theory has been in the field of stable homotopy theory, with the construction of a particular extraordinary cohomology theory associated to the construction for a given prime p. As part of general machinery for formal groups, a cohomology theory with spectrum is set up for the Lubin–Tate formal group, which also goes by the names of Morava E-theory or completed Johnson–Wilson theory.[4]
References
- ↑ Manin, Yu. I.; Panchishkin, A. A. (2007). Introduction to Modern Number Theory. Encyclopaedia of Mathematical Sciences 49 (Second ed.). p. 168. ISBN 978-3-540-20364-3. ISSN 0938-0396. Zbl 1079.11002.
- ↑ 2.0 2.1 Koch, Helmut (1997). Algebraic Number Theory. Encycl. Math. Sci. 62 (2nd printing of 1st ed.). Springer-Verlag. pp. 62–63. ISBN 3-540-63003-1. Zbl 0819.11044.
- ↑ e.g. Serre (1967). Hazewinkel, Michiel (1975). "Local class field theory is easy". Advances in Math. 18 (2): 148–181. doi:10.1016/0001-8708(75)90156-5. Zbl 0312.12022.
- ↑ http://www.math.harvard.edu/~lurie/252xnotes/Lecture22.pdf
- de Shalit, Ehud (1987), Iwasawa theory of elliptic curves with complex multiplication. p-adic L functions, Perspectives in Mathematics 3, Academic Press, ISBN 0-12-210255-X, Zbl 0674.12004
- Iwasawa, Kenkichi (1986), Local class field theory, Oxford Mathematical Monographs, The Clarendon Press Oxford University Press, ISBN 978-0-19-504030-2, MR 863740, Zbl 0604.12014
- Lubin, Jonathan; Tate, John (1965), "Formal complex multiplication in local fields", Annals of Mathematics. Second Series 81: 380–387, ISSN 0003-486X, JSTOR 1970622, MR 0172878, Zbl 0128.26501
- Lubin, Jonathan; Tate, John (1966), "Formal moduli for one-parameter formal Lie groups", Bulletin de la Société Mathématique de France 94: 49–59, ISSN 0037-9484, MR 0238854, Zbl 0156.04105
- Neukirch, Jürgen (1999), Algebraic Number Theory, Grundlehren der mathematischen Wissenschaften 322, Berlin: Springer-Verlag, ISBN 978-3-540-65399-8, Zbl 0956.11021, MR 1697859
- Serre, Jean-Pierre (1967), "Local class field theory", in Cassels, J.W.S.; Fröhlich, Albrecht, Algebraic Number Theory (Proc. Instructional Conf., Brighton, 1965), Academic Press, pp. 128–161, MR 0220701, Zbl 0153.07403
External links
- Lurie, J. (2010), Lubin–Tate theory