Lower critical solution temperature
The lower critical solution temperature (LCST) or lower consolute temperature is the critical temperature below which the components of a mixture are miscible for all compositions.[1] The word lower indicates that the LCST is a lower bound to a temperature interval of partial miscibility, or miscibility for certain compositions only.
The phase behavior of polymer solutions is an important property involved in the development and design of most polymer-related processes. Partially miscible polymer solutions often exhibit two solubility boundaries, the upper critical solution temperature (UCST) and the lower critical solution temperature (LCST), which both depend on the molar mass and the pressure. At temperatures below LCST, the system is completely miscible in all proportions, whereas above LCST partial liquid miscibility occurs.[2][3]
In the phase diagram of the mixture components, the LCST is the shared minimum of the concave up spinodal and binodal (or coexistence) curves. It is in general pressure dependent, increasing as a function of increased pressure.
For small molecules, the existence of an LCST is much less common than the existence of an upper critical solution temperature (UCST), but some cases do exist. For example, the system triethylamine-water has an LCST of 19 °C, so that these two substances are miscible in all proportions below 19 °C but not at higher temperatures.[4][5] The nicotine-water system has an LCST of 61 °C, and also a UCST of 210 °C at pressures high enough for liquid water to exist at that temperature. The components are therefore miscible in all proportions below 61 °C and above 210 °C (at high pressure), and partially miscible in the interval from 61 to 210 °C.[4][5]
Polymer-solvent mixtures
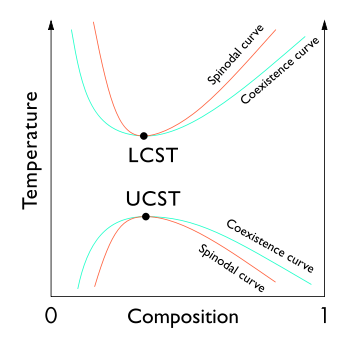
Some polymer solutions have an LCST at temperatures higher than the UCST. As shown in the diagram, this means that there is a temperature interval of complete miscibility, with partial miscibility at both higher and lower temperatures.[6]
In the case of polymer solutions, the LCST also depends on polymer degree of polymerization, polydispersity and branching[7] as well as on the polymer's composition and architecture.[8] A prominent polymer possessing an LCST is Poly(N-isopropylacrylamide) in water, which undergoes a reversible collapse transition related to the LCST at 33 °C.
The LCST depends on the polymer preparation and in the case of copolymers, the monomer ratios, as well as the hydrophobic or hydrophilic nature of the polymer.
Physical basis
A key physical factor which distinguishes the LCST from other mixture behavior is that the LCST phase separation is driven by unfavorable entropy of mixing.[9] Since mixing of the two phases is spontaneous below the LCST and not above, the Gibbs free energy change (ΔG) for the mixing of these two phases is negative below the LCST and positive above, and the entropy change ΔS = – (dΔG/dT) is negative for this mixing process. This is in contrast to the more common and intuitive case in which entropies drive mixing due to the increased volume accessible to each component upon mixing.
In general, the unfavorable entropy of mixing responsible for the LCST has one of two physical origins. The first is associating interactions between the two components such as strong polar interactions or hydrogen bonds, which prevent random mixing. For example in the triethylamine-water system, the amine molecules cannot form hydrogen bonds with each other but only with water molecules, so in solution they remain associated to water molecules with loss of entropy. The mixing which occurs below 19 °C is due not to entropy but to the enthalpy of formation of the hydrogen bonds.
The second physical factor which can lead to an LCST is compressibility effects, especially in polymer-solvent systems.[9] For nonpolar systems such as polystyrene in cyclohexane, phase separation has been observed in sealed tubes (at high pressure) at temperatures approaching the liquid-vapor critical point of the solvent. At such temperatures the solvent expands much more rapidly than the polymer, whose segments are covalently linked. Mixing therefore requires contraction of the solvent for compatibility of the polymer, resulting in a loss of entropy.[6]
Theory
Within statistical mechanics, the LCST may be modeled theoretically via the lattice fluid model, an extension of Flory–Huggins solution theory, that incorporates vacancies, and thus accounts for variable density and compressibility effects.[9]
Prediction of θ (lower critical solution temperature) LCST
There are three groups of methods for correlating and predicting LCSTs. The first group proposes models that are based on a solid theoretical background using liquid–liquid or vapor–liquid experimental data. These methods require experimental data to adjust the unknown parameters, resulting in limited predictive ability .[10] Another approach uses empirical equations that correlate θ(LCST) with physicochemical properties such as density, critical properties etc., but suffers from the disadvantage that these properties are not always available.[11][12] A new approach proposed by Liu and Zhong develops linear models for the prediction of θ(LCST) using molecular connectivity indices, which depends only on the solvent and polymer structures.[13][14] The latter approach has proven to be a very useful technique in quantitative structure–activity/property relationships (QSAR/QSPR) research for polymers and polymer solutions. QSAR/QSPR studies constitute an attempt to reduce the trial-and-error element in the design of compounds with desired activity/properties by establishing mathematical relationships between the activity/property of interest and measurable or computable parameters, such as topological, physicochemical, stereochemistry, or electronic indices. More recently QSPR models for the prediction of the θ (LCST) using molecular (electronic, physicochemical etc.) descriptors have been published.[15] Using validated robust QSPR models, experimental time and effort can be reduced significantly as reliable estimates of θ(LCST) for polymer solutions can be obtained before they are actually synthesized in the laboratory.
See also
Upper critical solution temperature
Coil-globule transition
References
- ↑ "IUPAC Compendium of Chemical Terminology". Retrieved 2009-03-05.
- ↑ Charlet G, Delmas G (1981) Polymer 22:1181–1189
- ↑ Charlet G, Ducasse R, Delmas G (1981) Polymer 22:1190–1198
- ↑ 4.0 4.1 P.W. Atkins and J. de Paula, "Atkins' Physical Chemistry" (8th edn, W.H. Freeman 2006) p. 187
- ↑ 5.0 5.1 M. A. White, Properties of Materials (Oxford University Press 1999) p. 175
- ↑ 6.0 6.1 Cowie, J.M.G. "Polymers: Chemistry and Physics of Modern Materials" (2nd edn, Blackie 1991) p.174-177
- ↑ S. Carter, B. Hunt, S. Rimmer, Macromolecules 38 4595 (2005);S. Rimmer, S. Carter, R. Rutkaite, J. W.Haycock, L. Swanson Soft Matter, 3 971 (2007)
- ↑ M. A. Ward, T. K. Georgiou, Journal of Polymer Science Part A: Polymer Chemistry 48 775 (2010)
- ↑ 9.0 9.1 9.2 Sanchez, IC and Stone, MT, "Statistical Thermodynamics of Polymer Solutions and Blends" in Polymer Blends Volume 1: Formulation. Edited by D.R. Paul and C. B. Bucknall, 2000 John Wiley & Sons, Inc.
- ↑ Chang BH, Bae CY (1998) Polymer 39:6449–6454
- ↑ Wang F, Saeki S, Yamaguchi T (1999) Polymer 40:2779–2785
- ↑ Vetere A (1998) Ind Eng Chem Res 37:4463–4469
- ↑ Liu H, Zhong C (2005) Eur Polym J 41:139–147
- ↑ Liu H, Zhong C (2005) Ind Eng Chem Res 44:634–638
- ↑ G. Melagraki, A. Afantitis, H. Sarimveis, P.A. Koutentis, J. Markopoulos and O. Igglessi-Markopoulou J Mol Model (2007) 13: 55–64 DOI 10.1007/s00894-006-0125-z