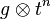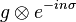Loop algebra

In mathematics, loop algebras are certain types of Lie algebra, of particular interest in theoretical physics.

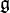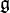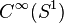If $\mathfrak{g}$ is a Lie algebra, the tensor product of $\mathfrak{g}$ with $C^\infty(S^1)$ ,

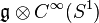\mathfrak{g}\otimes C^\infty(S^1)

the algebra of (complex) smooth functions over the circle manifold S¹ is an infinite-dimensional Lie algebra with the Lie bracket given by

[g_1\otimes f_1,g_2 \otimes f_2]=[g_1,g_2]\otimes f_1 f_2

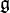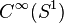Here g₁ and g₂ are elements of $\mathfrak{g}$ and f₁ and f₂ are elements of $C^\infty(S^1)$ .

This isn't precisely what would correspond to the direct product of infinitely many copies of 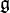$\mathfrak{g}$ , one for each point in S¹, because of the smoothness restriction. Instead, it can be thought of in terms of smooth map from S¹ to 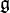$\mathfrak{g}$ ; a smooth parameterized loop in 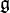$\mathfrak{g}$ , in other words. This is why it is called the loop algebra.

We can take the Fourier transform on this loop algebra by defining

g\otimes t^n

g\otimes e^{-in\sigma}

where

0 ≤ σ <2π

is a coordinatization of S¹.

If 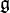$\mathfrak{g}$ is a semisimple Lie algebra, then a nontrivial central extension of its loop algebra gives rise to an affine Kac–Moody algebra.

Similarly, a set of all smooth maps from S¹ to a Lie group G forms an infinite-dimensional Lie group (Lie group in the sense we can define functional derivatives over it) called the loop group. The Lie algebra of a loop group is the corresponding loop algebra.