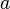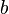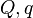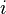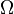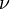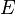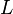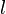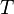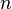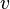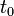Longitude of the ascending node

The longitude of the ascending node.

The longitude of the ascending node (☊ or Ω) is one of the orbital elements used to specify the orbit of an object in space. It is the angle from a reference direction, called the origin of longitude, to the direction of the ascending node, measured in a reference plane.^[1] Commonly used reference planes and origins of longitude include:

• For a geocentric orbit, Earth's equatorial plane as the reference plane, and the First Point of Aries as the origin of longitude. In this case, the longitude is also called the right ascension of the ascending node, or RAAN. The angle is measured eastwards (or, as seen from the north, counterclockwise) from the First Point of Aries to the node.^[2][3]
• For a heliocentric orbit, the ecliptic as the reference plane, and the First Point of Aries as the origin of longitude. The angle is measured counterclockwise (as seen from north of the ecliptic) from the First Point of Aries to the node.^[2]
• For an orbit outside the Solar System, the plane through the primary perpendicular to a line through the observer and the primary (called the plane of the sky) as the reference plane, and north, i.e., the perpendicular projection of the direction from the observer to the North Celestial Pole onto the plane of the sky, as the origin of longitude. The angle is measured eastwards (or, as seen by the observer, counterclockwise) from north to the node.^{[4], pp. 40, 72, 137; [5], chap. 17.}

In the case of a binary star known only from visual observations, it is not possible to tell which node is ascending and which is descending. In this case the orbital parameter which is recorded is the longitude of the node, Ω, which is the longitude of whichever node has a longitude between 0 and 180 degrees.^{[5], chap. 17;[4], p. 72.}

Calculation from state vectors

In astrodynamics, the longitude of the ascending node can be calculated from the specific relative angular momentum vector h as follows:

Here, n=<n_x, n_y, n_z> is a vector pointing towards the ascending node. The reference plane is assumed to be the xy-plane, and the origin of longitude is taken to be the positive x-axis. k is the unit vector (0, 0, 1), which is the normal vector to the xy reference plane.

For non-inclined orbits (with inclination equal to zero), Ω is undefined. For computation it is then, by convention, set equal to zero; that is, the ascending node is placed in the reference direction, which is equivalent to letting n point towards the positive x-axis.

See also

• Kepler orbits
• Equinox
• Orbital node
• perturbation of the orbital plane can cause revolution of the ascending node

References

1. ↑ Parameters Describing Elliptical Orbits, web page, accessed May 17, 2007.
2. ↑ 2.0 2.1 Orbital Elements and Astronomical Terms, Robert A. Egler, Dept. of Physics, North Carolina State University. Web page, accessed May 17, 2007.
3. ↑ Keplerian Elements Tutorial, amsat.org, accessed May 17, 2007.
4. ↑ 4.0 4.1 The Binary Stars, R. G. Aitken, New York: Semi-Centennial Publications of the University of California, 1918.
5. ↑ 5.0 5.1 Celestial Mechanics, Jeremy B. Tatum, on line, accessed May 17, 2007.