Long Josephson junction

In superconductivity, a long Josephson junction (LJJ) is a Josephson junction which has one or more dimensions longer than the Josephson penetration depth 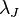$\lambda_J$ . This definition is not strict.

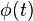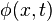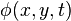In terms of underlying model a short Josephson junction is characterized by the Josephson phase $\phi(t)$ , which is only a function of time, but not of coordinates i.e. the Josephson junction is assumed to be point-like in space. In contrast, in a long Josephson junction the Josephson phase can be a function of one or two spatial coordinates, i.e., $\phi(x,t)$ or $\phi(x,y,t)$ .

Simple model: the sine-Gordon equation

The simplest and the most frequently used model which describes the dynamics of the Josephson phase $\phi$ in LJJ is the so-called perturbed sine-Gordon equation. For the case of 1D LJJ it looks like:

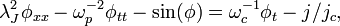
\lambda_J^2\phi_{xx}-\omega_p^{-2}\phi_{tt}-\sin(\phi) =\omega_c^{-1}\phi_t - j/j_c,

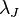where subscripts $x$ and $t$ denote partial derivatives with respect to $x$ and $t$ , $\lambda_J$ is the Josephson penetration depth, 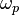$\omega_p$ is the Josephson plasma frequency, 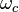$\omega_c$ is the so-called characteristic frequency and 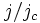$j/j_c$ is the bias current density 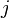$j$ normalized to the critical current density 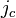$j_c$ . In the above equation, the r.h.s. is considered as perturbation.

Usually for theoretical studies one uses normalized sine-Gordon equation:

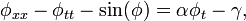
\phi_{xx}-\phi_{tt}-\sin(\phi)=\alpha\phi_t - \gamma,

where spatial coordinate is normalized to the Josephson penetration depth 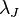$\lambda_J$ and time is normalized to the inverse plasma frequency 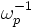$\omega_p^{-1}$ . The parameter 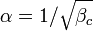$\alpha=1/\sqrt{\beta_c}$ is the dimensionless damping parameter ( 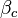$\beta_c$ is McCumber-Stewart parameter), and, finally, 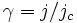$\gamma=j/j_c$ is a normalized bias current.

Important solutions

Small amplitude plasma waves. $\phi(x,t)=A\exp[i(kx-\omega t)]$

Soliton (aka fluxon, Josephson vortex):^[1]

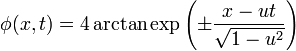
\phi(x,t)=4\arctan\exp\left(\pm\frac{x-ut}{\sqrt{1-u^2}}\right)

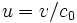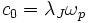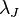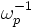Here $x$ , $t$ and $u=v/c_0$ are the normalized coordinate, normalized time and normalized velocity. The physical velocity $v$ is normalized to the so-called Swihart velocity $c_0=\lambda_J\omega_p$ , which represent a typical unit of velocity and equal to the unit of space $\lambda_J$ divided by unit of time $\omega_p^{-1}$ .

References

↑ M. Tinkham, Introduction to superconductivity, 2nd ed., Dover New York (1996).