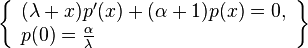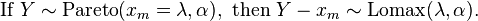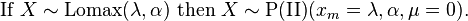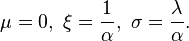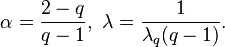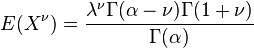Lomax distribution

Lomax
Parameters

\lambda >0 scale (real)

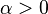\alpha > 0 shape (real)
Support x \ge 0
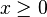PDF {\alpha \over \lambda} \left[{1+ {x \over \lambda}}\right]^{-(\alpha+1)}
CDF 1- \left[{1+ {x \over \lambda}}\right]^{-\alpha}
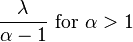Mean {\lambda \over {\alpha -1}} \text{ for } \alpha > 1
Otherwise undefined
Median \lambda (\sqrt[\alpha]{2} - 1)
Mode 0
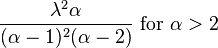Variance {{\lambda^2 \alpha} \over {(\alpha-1)^2(\alpha-2)}} \text{ for } \alpha > 2
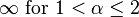\infty \text{ for } 1 < \alpha \le 2
Otherwise undefined
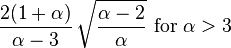Skewness \frac{2(1+\alpha)}{\alpha-3}\,\sqrt{\frac{\alpha-2}{\alpha}}\text{ for }\alpha>3\,
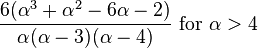Ex. kurtosis \frac{6(\alpha^3+\alpha^2-6\alpha-2)}{\alpha(\alpha-3)(\alpha-4)}\text{ for }\alpha>4\,

The Lomax distribution, conditionally also called the Pareto Type II distribution, is a heavy-tail probability distribution often used in business, economics, and actuarial modeling.[1][2] It is named after K. S. Lomax. It is essentially a Pareto distribution that has been shifted so that its support begins at zero.[3]

Characterization

Probability density function

The probability density function (pdf) for the Lomax distribution is given by

p(x) = {\alpha \over \lambda} \left[{1+ {x \over \lambda}}\right]^{-(\alpha+1)}, \qquad x \geq 0,

with shape parameter 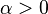\alpha>0 and scale parameter 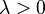\lambda>0. The density can be rewritten in such a way that more clearly shows the relation to the Pareto Type I distribution. That is:

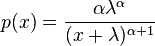p(x) = {{\alpha \lambda^\alpha} \over { (x+\lambda)^{\alpha+1}}}.

Differential equation

The pdf of the Lomax distribution is a solution to the following differential equation:

\left\{\begin{array}{l} (\lambda +x) p'(x)+(\alpha +1) p(x)=0, \\ p(0)=\frac{\alpha}{\lambda} \end{array}\right\}

Relation to the Pareto distribution

The Lomax distribution is a Pareto Type I distribution shifted so that its support begins at zero. Specifically:

\text{If } Y \sim \mbox{Pareto}(x_m = \lambda, \alpha), \text{ then } Y - x_m \sim \mbox{Lomax}(\lambda,\alpha).

The Lomax distribution is a Pareto Type II distribution with xm=λ and μ=0:[4]

\text{If } X \sim \mbox{Lomax}(\lambda,\alpha) \text{ then } X \sim \text{P(II)}(x_m = \lambda, \alpha, \mu=0).

Relation to generalized Pareto distribution

The Lomax distribution is a special case of the generalized Pareto distribution. Specifically:

\mu = 0,~ \xi = {1 \over \alpha},~ \sigma = {\lambda \over \alpha} .

Relation to q-exponential distribution

The Lomax distribution is a special case of the q-exponential distribution. The q-exponential extends this distribution to support on a bounded interval. The Lomax parameters are given by:

\alpha = { {2-q} \over {q-1}}, ~ \lambda = {1 \over \lambda_q (q-1)} .

Non-central moments

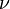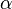The \nuth non-central moment E[X^\nu] exists only if the shape parameter \alpha strictly exceeds 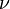\nu, when the moment has the value

E(X^\nu) = \frac{ \lambda^\nu \Gamma(\alpha-\nu)\Gamma(1+\nu)}{\Gamma(\alpha)}

See also

References

  1. ↑ Lomax, K. S. (1954) "Business Failures; Another example of the analysis of failure data". Journal of the American Statistical Association, 49, 847–852. JSTOR 2281544
  2. ↑ Johnson, N.L., Kotz, S., Balakrishnan, N. (1994) Continuous Univariate Distributions, Volume 1, 2nd Edition, Wiley. ISBN 0-471-58495-9 (pages 575, 602)
  3. ↑ Van Hauwermeiren M and Vose D (2009). A Compendium of Distributions [ebook]. Vose Software, Ghent, Belgium. Available at www.vosesoftware.com. Accessed 07/07/11
  4. ↑ Kleiber, Christian; Kotz, Samuel (2003), Statistical Size Distributions in Economics and Actuarial Sciences, Wiley Series in Probability and Statistics 470, John Wiley & Sons, p. 60, ISBN 9780471457169.