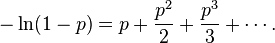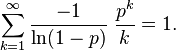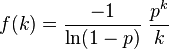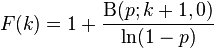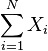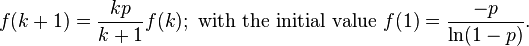Logarithmic distribution

Logarithmic
Probability mass function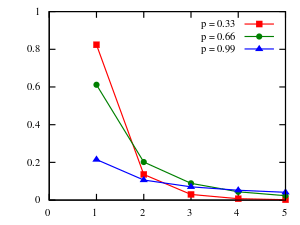

The function is only defined at integer values. The connecting lines are merely guides for the eye.

Cumulative distribution function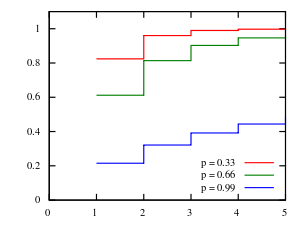
Parameters 0 < p < 1\!
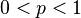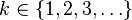Support k \in \{1,2,3,\dots\}\!
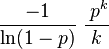pmf \frac{-1}{\ln(1-p)} \; \frac{\;p^k}{k}\!
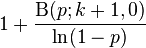CDF 1 + \frac{\Beta(p;k+1,0)}{\ln(1-p)}\!
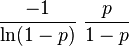Mean \frac{-1}{\ln(1-p)} \; \frac{p}{1-p}\!
Mode 1
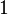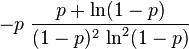Variance -p \;\frac{p + \ln(1-p)}{(1-p)^2\,\ln^2(1-p)} \!
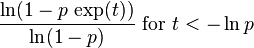MGF \frac{\ln(1 - p\,\exp(t))}{\ln(1-p)}\text{ for }t<-\ln p\,
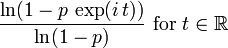CF \frac{\ln(1 - p\,\exp(i\,t))}{\ln(1-p)}\text{ for }t\in\mathbb{R}\!
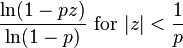PGF \frac{\ln(1-pz)}{\ln(1-p)}\text{ for }|z|<\frac1p

In probability and statistics, the logarithmic distribution (also known as the logarithmic series distribution or the log-series distribution) is a discrete probability distribution derived from the Maclaurin series expansion

-\ln(1-p) = p + \frac{p^2}{2} + \frac{p^3}{3} + \cdots.

From this we obtain the identity

\sum_{k=1}^{\infty} \frac{-1}{\ln(1-p)} \; \frac{p^k}{k} = 1.

This leads directly to the probability mass function of a Log(p)-distributed random variable:

f(k) = \frac{-1}{\ln(1-p)} \; \frac{p^k}{k}

for k ≥ 1, and where 0 < p < 1. Because of the identity above, the distribution is properly normalized.

The cumulative distribution function is

F(k) = 1 + \frac{\Beta(p; k+1,0)}{\ln(1-p)}

where B is the incomplete beta function.

A Poisson compounded with Log(p)-distributed random variables has a negative binomial distribution. In other words, if N is a random variable with a Poisson distribution, and Xi, i = 1, 2, 3, ... is an infinite sequence of independent identically distributed random variables each having a Log(p) distribution, then

\sum_{i=1}^N X_i

has a negative binomial distribution. In this way, the negative binomial distribution is seen to be a compound Poisson distribution.

R. A. Fisher described the logarithmic distribution in a paper that used it to model relative species abundance.[1]

The probability mass function ƒ of this distribution satisfies the recurrence relation

f(k+1) = \frac{kp}{k+1}f(k); \text{ with the initial value } f(1) = \frac{-p}{\ln(1-p)}.

See also

References

  1. ↑ Fisher, R. A.; Corbet, A. S.; Williams, C. B. (1943). "The Relation Between the Number of Species and the Number of Individuals in a Random Sample of an Animal Population". Journal of Animal Ecology 12 (1): 42–58. doi:10.2307/1411. JSTOR 1411.

Further reading