Log-space transducer

A log space transducer (LST) is a type of Turing machine used for log-space reductions.

A log space transducer, $M$ , has three tapes:

A read-only input tape.
A read/write work tape (bounded to at most 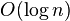$O(\log n)$ symbols).
A write-only, write-once output tape.

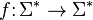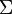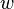$M$ will be designed to compute a log-space computable function $f\colon \Sigma^\ast \rightarrow \Sigma^\ast$ (where $\Sigma$ is the alphabet of both the input and output tapes). If $M$ is executed with $w$ on its input tape, when the machine halts, it will have 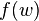$f(w)$ remaining on its output tape.

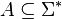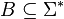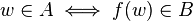A language $A \subseteq \Sigma^\ast$ is said to be log-space reducible to a language $B \subseteq \Sigma^\ast$ if there exists a log-space computable function, $f$ , which will convert an input from problem $A$ into an input to problem $B$ . I.E. $w \in A \iff f(w) \in B$ .

This seems like a rather convoluted idea, but it has two useful properties that are desirable for a reduction:

The property of transitivity holds. (A reduces to B and B reduces to C implies A reduces to C).
If A reduces to B, and B is in L, then we know A is in L.

Transitivity holds because it is possible to feed the output tape of one reducer (A->B) to another (B->C). At first glance, this seems incorrect because the A->C reducer needs to store the output tape from the A->B reducer onto the work tape in order to feed it into the B->C reducer, but this is not true. Each time the B->C reducer needs to access its input tape, the A->C reducer can re-run the A->B reducer, and so the output of the A->B reducer never needs to be stored entirely at once.

References

Szepietowski, Andrzej (1994), Turing Machines with Sublogarithmic Space , Springer Press, ISBN 3-540-58355-6. Retrieved on 2008-12-03.
Sipser, Michael (2012), Introduction to the Theory of Computation, Cengage Learning, ISBN 978-0-619-21764-8.