Log-normal distribution
|
Probability density function
| |
|
Cumulative distribution function
| |
| Notation |
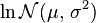 |
|---|---|
| Parameters |
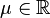 — location, — location, 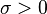 — scale — scale |
| Support |
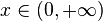 |
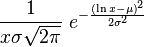 | |
| CDF |
![\frac12 + \frac12\,\mathrm{erf}\Big[\frac{\ln x-\mu}{\sqrt{2}\sigma}\Big]](../I/m/2049e219bac8f47a956631cd9eed2b7d.png) |
| Mean |
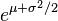 |
| Median |
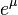 |
| Mode |
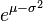 |
| Variance |
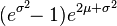 |
| Skewness |
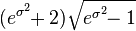 |
| Ex. kurtosis |
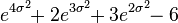 |
| Entropy |
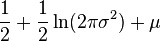 |
| MGF | (defined only on the negative half-axis, see text) |
| CF |
representation 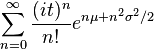 is asymptotically divergent but sufficient for numerical purposes is asymptotically divergent but sufficient for numerical purposes |
| Fisher information |
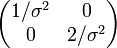 |
In probability theory, a log-normal (or lognormal) distribution is a continuous probability distribution of a random variable whose logarithm is normally distributed. Thus, if the random variable  is log-normally distributed, then
is log-normally distributed, then 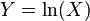 has a normal distribution. Likewise, if
has a normal distribution. Likewise, if  has a normal distribution, then
has a normal distribution, then 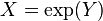 has a log-normal distribution. A random variable which is log-normally distributed takes only positive real values.
has a log-normal distribution. A random variable which is log-normally distributed takes only positive real values.
The distribution is occasionally referred to as the Galton distribution or Galton's distribution, after Francis Galton.[1] The log-normal distribution also has been associated with other names, such as McAlister, Gibrat and Cobb–Douglas.[1]
A variable might be modeled as log-normal if it can be thought of as the multiplicative product of many independent random variables, each of which is positive. This is justified by considering the central limit theorem in the log domain.
For example, in finance, the variable could represent the compound return from a sequence of many trades, each expressed as its return + 1; or a long-term discount factor can be derived from the product of short-term discount factors. This was observed by Gilbrat, who claimed that the size of a firm and its growth rate are independent, and called the associated central limit tendency "the law of proportionate effect."[2]
In wireless communication, the delay caused by shadowing or slow fading from random objects is often assumed to be log-normally distributed: see log-distance path loss model.
The log-normal distribution is the maximum entropy probability distribution for a random variate  for which the mean and variance of
for which the mean and variance of 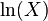 are specified.[3]
are specified.[3]
Notation
Given a log-normally distributed random variable  and two parameters
and two parameters  and
and  that are, respectively, the mean and standard deviation of the variable’s natural logarithm (by definition, the variable’s logarithm is normally distributed), we can write
that are, respectively, the mean and standard deviation of the variable’s natural logarithm (by definition, the variable’s logarithm is normally distributed), we can write  as
as
with  a standard normal variable.
a standard normal variable.
This relationship is true regardless of the base of the logarithmic or exponential function. If 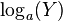 is normally distributed, then so is
is normally distributed, then so is 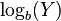 , for any two positive numbers
, for any two positive numbers 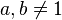 . Likewise, if
. Likewise, if 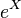 is log-normally distributed, then so is
is log-normally distributed, then so is 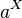 , where
, where  is a positive number
is a positive number 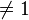 .
.
On a logarithmic scale,  and
and  can be called the location parameter and the scale parameter, respectively.
can be called the location parameter and the scale parameter, respectively.
In contrast, the mean, standard deviation, and variance of the non-logarithmized sample values are respectively denoted  , s.d., and
, s.d., and  in this article. The two sets of parameters can be related as (see also Arithmetic moments below)[4]
in this article. The two sets of parameters can be related as (see also Arithmetic moments below)[4]
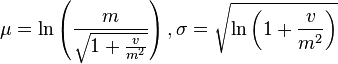 .
.
Characterization
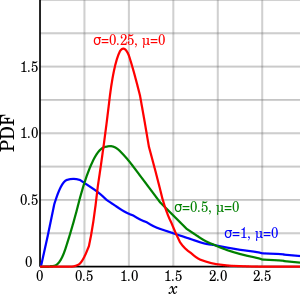
Probability density function
The probability density function of a log-normal distribution is:[1]
This follows by applying the change-of-variables rule on the density function of a normal distribution.
Cumulative distribution function
The cumulative distribution function is
where erfc is the complementary error function, and Φ is the cumulative distribution function of the standard normal distribution.
Characteristic function and moment generating function
All moments of the log-normal distribution exist and it holds that: ![\operatorname{E}[X^n]=\mathrm{e}^{n\mu+\frac{n^2\sigma^2}{2}}](../I/m/e356f2a0d61debc3e03df9641fb42fbe.png) (which can be derived by letting
(which can be derived by letting 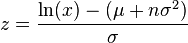 within the integral). However, the expected value
within the integral). However, the expected value ![\operatorname{E}[e^{t X}]](../I/m/c900dc8073d5c4377e6c7c10c903e8cc.png) is not defined for any positive value of the argument
is not defined for any positive value of the argument  as the defining integral diverges. In consequence
the moment generating function is not defined.[5] The last is related to the fact that the lognormal distribution is not uniquely determined by its moments.
as the defining integral diverges. In consequence
the moment generating function is not defined.[5] The last is related to the fact that the lognormal distribution is not uniquely determined by its moments.
Similarly, the characteristic function ![\operatorname{E}[e^{i t X}]](../I/m/7f80964ac270ec4485d815324f37f904.png) is not defined in the half complex plane and therefore it is not analytic in the origin. In consequence, the characteristic function of the log-normal distribution cannot be represented as an infinite convergent series.[6] In particular, its Taylor formal series
is not defined in the half complex plane and therefore it is not analytic in the origin. In consequence, the characteristic function of the log-normal distribution cannot be represented as an infinite convergent series.[6] In particular, its Taylor formal series 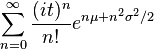 diverges. However, a number of alternative divergent series representations have been obtained[6][7][8][9]
diverges. However, a number of alternative divergent series representations have been obtained[6][7][8][9]
A closed-form formula for the characteristic function 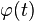 with
with  in the domain of convergence is not known. A relatively simple approximating formula is available in closed form and given by[10]
in the domain of convergence is not known. A relatively simple approximating formula is available in closed form and given by[10]
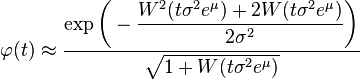
where  is the Lambert W function. This approximation is derived via an asymptotic method but it stays sharp all over the domain of convergence of
is the Lambert W function. This approximation is derived via an asymptotic method but it stays sharp all over the domain of convergence of 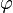 .
.
Properties
Location and scale
The location and scale parameters of a log-normal distribution, i.e.  and
and  , are more readily treated using the geometric mean,
, are more readily treated using the geometric mean, ![\mathrm{GM}[X]](../I/m/fa6f2ad9f679faf9ab2b05d74f31a180.png) , and the geometric standard deviation,
, and the geometric standard deviation, ![\mathrm{GSD}[X]](../I/m/cbe69ac233b336f8fe993615ef9b2aa7.png) , rather than the arithmetic mean,
, rather than the arithmetic mean, ![\mathrm{E}[X]](../I/m/1f11fa3c09b764cba755da9984f73987.png) , and the arithmetic standard deviation,
, and the arithmetic standard deviation, ![\mathrm{SD}[X]](../I/m/c8fc9c07cd70834a4e8253e90ef71b75.png) .
.
Geometric moments
The geometric mean of the log-normal distribution is ![\mathrm{GM}[X] = e^{\mu}](../I/m/0ed991a8016e6ea5f59e7fe50c9c081d.png) , and the geometric standard deviation is
, and the geometric standard deviation is ![\mathrm{GSD}[X] = e^{\sigma}](../I/m/76bb2bd03051c262bd417142ace91e71.png) .[11][12] By analogy with the arithmetic statistics, one can define a geometric variance,
.[11][12] By analogy with the arithmetic statistics, one can define a geometric variance, ![\mathrm{GVar}[X] = e^{\sigma^2}](../I/m/3b6cdfc539b12258fc9295867ceea982.png) , and a geometric coefficient of variation,[11]
, and a geometric coefficient of variation,[11] ![\mathrm{GCV}[X] = e^{\sigma} - 1](../I/m/9353771625a8711cd1eb09864b1758d4.png) .
.
Because the log-transformed variable 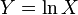 is symmetric and quantiles are preserved under monotonic transformations, the geometric mean of a log-normal distribution is equal to its median,
is symmetric and quantiles are preserved under monotonic transformations, the geometric mean of a log-normal distribution is equal to its median, ![\mathrm{Med}[X]](../I/m/47d73cec1e061caffa5906d5d7ce1f28.png) .[13]
.[13]
Note that the geometric mean is less than the arithmetic mean. This is due to the AM–GM inequality, and corresponds to the logarithm being convex down. In fact,
In finance the term 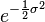 is sometimes interpreted as a convexity correction. From the point of view of stochastic calculus, this is the same correction term as in Itō's lemma for geometric Brownian motion.
is sometimes interpreted as a convexity correction. From the point of view of stochastic calculus, this is the same correction term as in Itō's lemma for geometric Brownian motion.
Arithmetic moments
The arithmetic mean, arithmetic variance, and arithmetic standard deviation of a log-normally distributed variable  are given by
are given by
respectively.
The location ( ) and scale (
) and scale ( ) parameters can be obtained if the arithmetic mean and the arithmetic variance are known; it is simpler if
) parameters can be obtained if the arithmetic mean and the arithmetic variance are known; it is simpler if  is computed first:
is computed first:
For any real or complex number  , the
, the  th moment of a log-normally distributed variable
th moment of a log-normally distributed variable  is given by[1]
is given by[1]
A log-normal distribution is not uniquely determined by its moments ![\operatorname{E}[X^k]](../I/m/ec3870e86fcb7e8daa8ce25a73d1326b.png) for
for 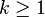 , that is, there exists some other distribution with the same moments for all
, that is, there exists some other distribution with the same moments for all  .[1] In fact, there is a whole family of distributions with the same moments as the log-normal distribution.
.[1] In fact, there is a whole family of distributions with the same moments as the log-normal distribution.
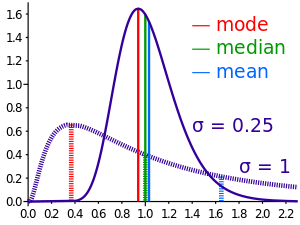
Mode and median
The mode is the point of global maximum of the probability density function. In particular, it solves the equation 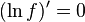 :
:
The median is such a point where 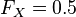 :
:
Arithmetic coefficient of variation
The arithmetic coefficient of variation ![\mathrm{CV}[X]](../I/m/bea26ffd7914e4e7a64c90ff1cc7abae.png) is the ratio
is the ratio ![\frac{\mathrm{SD}[X]}{\mathrm{E}[X]}](../I/m/ce03d03c7d0919166936b03319bb0014.png) (on the natural scale). For a log-normal distribution it is equal to
(on the natural scale). For a log-normal distribution it is equal to
Contrary to the arithmetic standard deviation, the arithmetic coefficient of variation is independent of the arithmetic mean.
Partial expectation
The partial expectation of a random variable  with respect to a threshold
with respect to a threshold  is defined as
is defined as 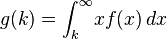 where
where 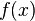 is the probability density function of
is the probability density function of  . Alternatively, and using the definition of conditional expectation, it can be written as
. Alternatively, and using the definition of conditional expectation, it can be written as ![g(k)=\operatorname{E}[X|X>k] P(X>k)](../I/m/5e50df0dcafaf501df8a059ee7574bd7.png) . For a log-normal random variable the partial expectation is given by:
. For a log-normal random variable the partial expectation is given by:
Where Phi is the normal cumulative distribution function. The derivation of the formula is provided in the discussion of this Wikipedia entry. The partial expectation formula has applications in insurance and economics, it is used in solving the partial differential equation leading to the Black–Scholes formula.
Other
A set of data that arises from the log-normal distribution has a symmetric Lorenz curve (see also Lorenz asymmetry coefficient).[14]
The harmonic  , geometric
, geometric  and arithmetic
and arithmetic  means of this distribution are related;[15] such relation is given by
means of this distribution are related;[15] such relation is given by
Log-normal distributions are infinitely divisible.[1]
Occurrence
The log-normal distribution is important in the description of natural phenomena. The reason is that for many natural processes of growth, growth rate is independent of size. This is also known as Gibrat's law, after Robert Gibrat (1904–1980) who formulated it for companies. It can be shown that a growth process following Gibrat's law will result in entity sizes with a log-normal distribution.[16] Examples include:
- In biology and medicine,
- Measures of size of living tissue (length, skin area, weight);[17]
- For highly communicable epidemics, such as SARS in 2003, if publication intervention is involved, the number of hospitalized cases is shown to satistfy the lognormal distribution with no free parameters if an entropy is assumed and the standard deviation is determined by the principle of maximum rate of entropy production.[18]
- The length of inert appendages (hair, claws, nails, teeth) of biological specimens, in the direction of growth;
- Certain physiological measurements, such as blood pressure of adult humans (after separation on male/female subpopulations)[19]

- Consequently, reference ranges for measurements in healthy individuals are more accurately estimated by assuming a log-normal distribution than by assuming a symmetric distribution about the mean.
- In colloidal chemistry and polymer chemistry
- Particle size distributions
- Molar mass distributions
- In hydrology, the log-normal distribution is used to analyze extreme values of such variables as monthly and annual maximum values of daily rainfall and river discharge volumes.[20]
- The image on the right illustrates an example of fitting the log-normal distribution to ranked annually maximum one-day rainfalls showing also the 90% confidence belt based on the binomial distribution. The rainfall data are represented by plotting positions as part of a cumulative frequency analysis.
- In social sciences and demographics
- In economics, there is evidence that the income of 97%–99% of the population is distributed log-normally.[21] (The distribution of higher-income individuals follows a Pareto distribution.[22])
- In finance, in particular the Black–Scholes model, changes in the logarithm of exchange rates, price indices, and stock market indices are assumed normal[23] (these variables behave like compound interest, not like simple interest, and so are multiplicative). However, some mathematicians such as Benoît Mandelbrot have argued [24] that log-Lévy distributions which possesses heavy tails would be a more appropriate model, in particular for the analysis for stock market crashes. Indeed stock price distributions typically exhibit a fat tail.[25]
- city sizes
- Technology
- In reliability analysis, the lognormal distribution is often used to model times to repair a maintainable system.[26]
- In wireless communication, "the local-mean power expressed in logarithmic values, such as dB or neper, has a normal (i.e., Gaussian) distribution." [27] Also, the random obstruction of radio signals due to large buildings and hills, called shadowing, is often modeled as a lognormal distribution.
- It has been proposed that coefficients of friction and wear may be treated as having a lognormal distribution [28]
- In spray process, such as droplet impact, the size of secondary produced droplet has a lognormal distribution, with the standard deviation :
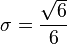 determined by the principle of maximum rate of entropy production[29] If the lognormal distribution is inserted into the Shannon entropy expression and if the rate of entropy production is maximized (principle of maximum rate of entropy production), then σ is given by :
determined by the principle of maximum rate of entropy production[29] If the lognormal distribution is inserted into the Shannon entropy expression and if the rate of entropy production is maximized (principle of maximum rate of entropy production), then σ is given by :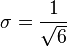 [29] and with this parameter the droplet size distribution for spray process is well predicted. It is an open question whether this value of σ has some generality for other cases, though for spreading of communicable epidemics, σ is shown also to take this value.[18]
[29] and with this parameter the droplet size distribution for spray process is well predicted. It is an open question whether this value of σ has some generality for other cases, though for spreading of communicable epidemics, σ is shown also to take this value.[18] - Particle size distributions produced by comminution with random impacts, such as in ball milling
- The file size distribution of publicly available audio and video data files (MIME types) follows a log-normal distribution over five orders of magnitude.[30]
Maximum likelihood estimation of parameters
For determining the maximum likelihood estimators of the log-normal distribution parameters μ and σ, we can use the same procedure as for the normal distribution. To avoid repetition, we observe that
where by 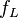 we denote the probability density function of the log-normal distribution and by
we denote the probability density function of the log-normal distribution and by 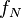 that of the normal distribution. Therefore, using the same indices to denote distributions, we can write the log-likelihood function thus:
that of the normal distribution. Therefore, using the same indices to denote distributions, we can write the log-likelihood function thus:
Since the first term is constant with regard to μ and σ, both logarithmic likelihood functions, 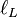 and
and 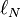 , reach their maximum with the same
, reach their maximum with the same  and
and  . Hence, using the formulas for the normal distribution maximum likelihood parameter estimators and the equality above, we deduce that for the log-normal distribution it holds that
. Hence, using the formulas for the normal distribution maximum likelihood parameter estimators and the equality above, we deduce that for the log-normal distribution it holds that
Multivariate log-normal
If 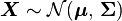 is a multivariate normal distribution then
is a multivariate normal distribution then 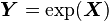 has a multivariate log-normal distribution[31] with mean
has a multivariate log-normal distribution[31] with mean
Related distributions
- If
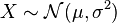 is a normal distribution, then
is a normal distribution, then 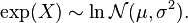
- If
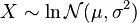 is distributed log-normally, then
is distributed log-normally, then 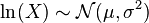 is a normal random variable.
is a normal random variable.
- If
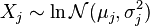 are
are  independent log-normally distributed variables, and
independent log-normally distributed variables, and 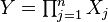 , then
, then  is also distributed log-normally:
is also distributed log-normally:
- Let
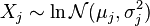 be independent log-normally distributed variables with possibly varying
be independent log-normally distributed variables with possibly varying  and
and  parameters, and
parameters, and 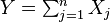 . The distribution of
. The distribution of  has no closed-form expression, but can be reasonably approximated by another log-normal distribution
has no closed-form expression, but can be reasonably approximated by another log-normal distribution  at the right tail.[32] Its probability density function at the neighborhood of 0 has been characterized[33] and it does not resemble any log-normal distribution. A commonly used approximation due to L.F. Fenton (but previously stated by R.I. Wilkinson and mathematical justified by Marlow[34]) is obtained by matching the mean and variance of another lognormal distribution:
at the right tail.[32] Its probability density function at the neighborhood of 0 has been characterized[33] and it does not resemble any log-normal distribution. A commonly used approximation due to L.F. Fenton (but previously stated by R.I. Wilkinson and mathematical justified by Marlow[34]) is obtained by matching the mean and variance of another lognormal distribution:
In the case that all 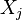 have the same variance parameter
have the same variance parameter 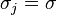 , these formulas simplify to
, these formulas simplify to
- If
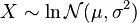 , then
, then 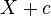 is said to have a shifted log-normal distribution with support
is said to have a shifted log-normal distribution with support 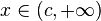 .
. ![\operatorname{E}[X+c] = \operatorname{E}[X]+c](../I/m/1bfd6d01182b4f6fe6ec7abd9a3cba62.png) ,
, ![\operatorname{Var}[X+c] = \operatorname{Var}[X]](../I/m/0f135f1cf2b0e0890a459269dfea6b69.png) .
.
- If
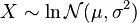 , then
, then 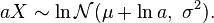
- If
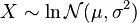 , then
, then 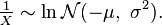
- If
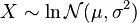 then
then 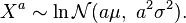 for
for 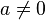
- Lognormal distribution is a special case of semi-bounded Johnson distribution
- If
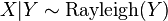 with
with 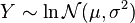 , then
, then 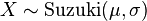 (Suzuki distribution)
(Suzuki distribution)
Similar distributions
A substitute for the log-normal whose integral can be expressed in terms of more elementary functions[35] can be obtained based on the logistic distribution to get an approximation for the CDF
This is a log-logistic distribution.
See also
- Log-distance path loss model
- Slow fading
- Stochastic volatility
Notes
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 Johnson, Norman L.; Kotz, Samuel; Balakrishnan, N. (1994), "14: Lognormal Distributions", Continuous univariate distributions. Vol. 1, Wiley Series in Probability and Mathematical Statistics: Applied Probability and Statistics (2nd ed.), New York: John Wiley & Sons, ISBN 978-0-471-58495-7, MR 1299979
- ↑ Kunio Shimizu and Edwin L. Crow, "History, Genesis, and Properties", ch. 1 in Crow and Shimizu (1988)
- ↑ Park, Sung Y.; Bera, Anil K. (2009). "Maximum entropy autoregressive conditional heteroskedasticity model" (PDF). Journal of Econometrics (Elsevier) 150 (2): 219–230. doi:10.1016/j.jeconom.2008.12.014. Retrieved 2011-06-02.
- ↑ "Lognormal mean and variance"
- ↑ Heyde, CC. (1963), "On a property of the lognormal distribution", Journal of the Royal Statistical Society, Series B (Methodological) 25 (2): 392–393, doi:10.1007/978-1-4419-5823-5_6
- ↑ 6.0 6.1 Holgate, P. (1989). "The lognormal characteristic function, vol. 18, pp. 4539–4548, 1989". Communications in Statistical – Theory and Methods 18 (12): 4539–4548. doi:10.1080/03610928908830173.
- ↑ Barakat, R. (1976). "Sums of independent lognormally distributed random variables". Journal of the Optical Society of America 66 (3): 211–216. doi:10.1364/JOSA.66.000211.
- ↑ Barouch, E.; Kaufman, GM.; Glasser, ML. (1986). "On sums of lognormal random variables" (PDF). Studies in Applied Mathematics 75 (1): 37–55.
- ↑ Leipnik, Roy B. (January 1991). "On Lognormal Random Variables: I – The Characteristic Function". Journal of the Australian Mathematical Society Series B 32 (3): 327–347. doi:10.1017/S0334270000006901.
- ↑ S. Asmussen, J.L. Jensen, L. Rojas-Nandayapa. "On the Laplace transform of the Lognormal distribution", Thiele centre preprint, (2013).
- ↑ 11.0 11.1 Kirkwood, Thomas BL (Dec 1979). "Geometric means and measures of dispersion". Biometrics 35 (4): 908–9. doi:10.2307/2530139.
- ↑ Limpert, E; Stahel, W; Abbt, M (2001). "Lognormal distributions across the sciences: keys and clues". BioScience 51 (5): 341–352. doi:10.1641/0006-3568(2001)051[0341:LNDATS]2.0.CO;2.
- ↑ Daly, Leslie E.; Bourke, Geoffrey Joseph (2000). Interpretation and uses of medical statistics (5th ed.). Wiley-Blackwell. p. 89. doi:10.1002/9780470696750. ISBN 978-0-632-04763-5.
- ↑ Damgaard, Christian; Weiner, Jacob (2000). "Describing inequality in plant size or fecundity". Ecology 81 (4): 1139–1142. doi:10.1890/0012-9658(2000)081[1139:DIIPSO]2.0.CO;2.
- ↑ Rossman, Lewis A (July 1990). "Design stream flows based on harmonic means". J Hydraulic Engineering 116 (7): 946–950. doi:10.1061/(ASCE)0733-9429(1990)116:7(946).
- ↑ Sutton, John (Mar 1997). "Gibrat's Legacy". Journal of Economic Literature 32 (1): 40–59. JSTOR 2729692.
- ↑ Huxley, Julian S. (1932). Problems of relative growth. London. ISBN 0-486-61114-0. OCLC 476909537.
- ↑ 18.0 18.1 Wang, WB; Wang, CF; Wu, ZN; Hu, RF (2013). "Modelling the spreading rate of controlled communicable epidemics through an entropy-based thermodynamic model" 56 (11). SCIENCE CHINA Physics, Mechanics & Astronomy. pp. 2143–2150.
- ↑ Makuch, Robert W.; D.H. Freeman, M.F. Johnson (1979). "Justification for the lognormal distribution as a model for blood pressure". Journal of Chronic Diseases 32 (3): 245–250. doi:10.1016/0021-9681(79)90070-5. Retrieved 27 February 2012.
- ↑ Ritzema (ed.), H.P. (1994). Frequency and Regression Analysis (PDF). Chapter 6 in: Drainage Principles and Applications, Publication 16, International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. pp. 175–224. ISBN 90-70754-33-9.
- ↑ Clementi, Fabio; Gallegati, Mauro (2005) "Pareto's law of income distribution: Evidence for Germany, the United Kingdom, and the United States", EconWPA
- ↑ Wataru, Souma (2002-02-22). "Physics of Personal Income". arXiv:cond-mat/0202388.
- ↑ Black, F.; Scholes, M. (1973). "The Pricing of Options and Corporate Liabilities". Journal of Political Economy 81 (3): 637. doi:10.1086/260062.
- ↑ Mandelbrot, Benoit (2004). The (mis-)Behaviour of Markets. Basic Books. ISBN 9780465043552.
- ↑ Bunchen, P., Advanced Option Pricing, University of Sydney coursebook, 2007
- ↑ O'Connor, Patrick; Kleyner, Andre (2011). Practical Reliability Engineering. John Wiley & Sons. p. 35. ISBN 978-0-470-97982-2.
- ↑ http://wireless.per.nl/reference/chaptr03/shadow/shadow.htm
- ↑ Steele, C. (2008). "Use of the lognormal distribution for the coefficients of friction and wear". Reliability Engineering & System Safety 93 (10): 1574–2013. doi:10.1016/j.ress.2007.09.005.
- ↑ 29.0 29.1 Wu, Zi-Niu (July 2003). "Prediction of the size distribution of secondary ejected droplets by crown splashing of droplets impinging on a solid wall". Probabilistic Engineering Mechanics 18 (3): 241–249. doi:10.1016/S0266-8920(03)00028-6.
- ↑ Gros, C; Kaczor, G.; Markovic, D (2012). "Neuropsychological constraints to human data production on a global scale". The European Physical Journal B 85 (28). doi:10.1140/epjb/e2011-20581-3.
- ↑ Tarmast, Ghasem (2001). Multivariate Log–Normal Distribution (PDF). ISI Proceedings: 53rd Session. Seoul.
- ↑ Asmussen, S.; Rojas-Nandayapa, L. (2008). "Asymptotics of Sums of Lognormal Random Variables with Gaussian Copula". Statistics and Probability Letters 78 (16): 2709–2714. doi:10.1016/j.spl.2008.03.035.
- ↑ Gao, X.; Xu, H; Ye, D. (2009), "Asymptotic Behaviors of Tail Density for Sum of Correlated Lognormal Variables". International Journal of Mathematics and Mathematical Sciences, vol. 2009, Article ID 630857. doi:10.1155/2009/630857
- ↑ Marlow, NA. (Nov 1967). "A normal limit theorem for power sums of independent normal random variables". Bell System Technical Journal 46 (9): 2081–2089. doi:10.1002/j.1538-7305.1967.tb04244.x.
- ↑ Swamee, P. K. (2002). "Near Lognormal Distribution". Journal of Hydrologic Engineering 7 (6): 441–444. doi:10.1061/(ASCE)1084-0699(2002)7:6(441).
References
- Crow, Edwin L.; Shimizu, Kunio (Editors) (1988), Lognormal Distributions, Theory and Applications, Statistics: Textbooks and Monographs 88, New York: Marcel Dekker, Inc., pp. xvi+387, ISBN 0-8247-7803-0, MR 0939191, Zbl 0644.62014
- Aitchison, J. and Brown, J.A.C. (1957) The Lognormal Distribution, Cambridge University Press.
- E. Limpert, W. Stahel and M. Abbt (2001) Log-normal Distributions across the Sciences: Keys and Clues, BioScience, 51 (5), 341–352.
- Eric W. Weisstein et al. Log Normal Distribution at MathWorld. Electronic document, retrieved October 26, 2006.
- Holgate, P. (1989). "The lognormal characteristic function". Communications in Statistics - Theory and Methods 18 (12): 4539–4548. doi:10.1080/03610928908830173.
Further reading
- Brooks, Robert; Corson, Jon; Donal, Wales (1994). "The Pricing of Index Options When the Underlying Assets All Follow a Lognormal Diffusion". Advances in Futures and Options Research 7.
External links
| Wikimedia Commons has media related to Log-normal distribution. |
| ||||||||||||||

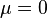 )
)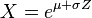
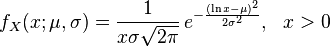
![F_X(x;\mu,\sigma) = \int_{0}^{x} f_X(\xi;\mu,\sigma) d\xi = \frac12 \left[ 1 + \operatorname{erf}\!\left(\frac{\ln x - \mu}{\sigma\sqrt{2}}\right) \right] = \frac12 \operatorname{erfc}\!\left(-\frac{\ln x - \mu}{\sigma\sqrt{2}}\right) = \Phi\bigg(\frac{\ln x - \mu}{\sigma}\bigg),](../I/m/a9aaebb577146a90c9432d4813fb8e0c.png)
![\begin{align}
\mathrm{E}[X] &= e^{\mu + \frac12 \sigma^2} &= e^{\mu} \cdot \sqrt{e^{\sigma^2}} &= \mathrm{GM}[X] \cdot \sqrt{\mathrm{GVar}[X]}.
\end{align}](../I/m/0bbfe8ba2cddb2171e1ef4df2f13f228.png)
![\begin{align}
& \operatorname{E}[X] = e^{\mu + \tfrac{1}{2}\sigma^2}, \\
& \operatorname{Var}[X] = (e^{\sigma^2} - 1) e^{2\mu + \sigma^2} = (e^{\sigma^2} - 1)(\operatorname{E}[X])^2, \\
& \operatorname{SD}[X] = \sqrt{\operatorname{Var}[X]} = e^{\mu + \tfrac{1}{2}\sigma^2}\sqrt{e^{\sigma^2} - 1}
= \operatorname{E}[X] \sqrt{e^{\sigma^2} - 1},
\end{align}](../I/m/0cb1ed290510999b9380a27afdbaf9ea.png)
![\begin{align}
\mu &= \ln(\operatorname{E}[X]) - \frac12 \ln\!\left(1 + \frac{\mathrm{Var}[X]}{(\operatorname{E}[X])^2}\right) = \ln(\operatorname{E}[X]) - \frac12 \sigma^2, \\
\sigma^2 &= \ln\!\left(1 + \frac{\operatorname{Var}[X]}{(\operatorname{E}[X])^2}\right).
\end{align}](../I/m/0ed02e0e945ce2bf85d23f0869a034f4.png)
![\operatorname{E}[X^s] = e^{s\mu + \frac12s^2\sigma^2}.](../I/m/ece38cf42f601f1285c033e5d7bbdc93.png)
![\mathrm{Mode}[X] = e^{\mu - \sigma^2}.](../I/m/cf8da3ba72bcc1f07730c021f6f895b6.png)
![\mathrm{Med}[X] = e^\mu\,.](../I/m/851eb4d1924fbec6d981f8c87d313adc.png)
![\mathrm{CV}[X] = \sqrt{e^{\sigma^2} - 1}.](../I/m/253da576d2966580f19964bfab9b7c56.png)
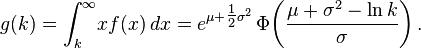
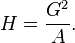
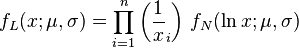
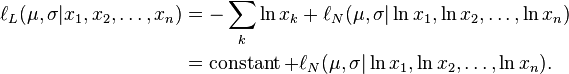
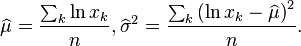
![\operatorname{E}[\boldsymbol Y]_i=e^{\mu_i+\frac{1}{2}\Sigma_{ii}} ,](../I/m/92ac934f8ad1267adfe21e93e7767412.png)
![\operatorname{Var}[\boldsymbol Y]_{ij}=e^{\mu_i+\mu_j + \frac{1}{2}(\Sigma_{ii}+\Sigma_{jj}) }( e^{\Sigma_{ij}} - 1) .](../I/m/cb45ba636e8834acf7c7a89e47d150a4.png)
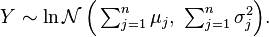
![\begin{align}
\sigma^2_Z &= \ln\!\left[ \frac{\sum e^{2\mu_j+\sigma_j^2}(e^{\sigma_j^2}-1)}{(\sum e^{\mu_j+\sigma_j^2/2})^2} + 1\right], \\
\mu_Z &= \ln\!\left[ \sum e^{\mu_j+\sigma_j^2/2} \right] - \frac{\sigma^2_Z}{2}.
\end{align}](../I/m/7abcdd1740efdd63d0f7a9348d58aa3f.png)
![\begin{align}
\sigma^2_Z &= \ln\!\left[ (e^{\sigma^2}-1)\frac{\sum e^{2\mu_j}}{(\sum e^{\mu_j})^2} + 1\right], \\
\mu_Z &= \ln\!\left[ \sum e^{\mu_j} \right] + \frac{\sigma^2}{2} - \frac{\sigma^2_Z}{2}.
\end{align}](../I/m/00fec5af852ce3480702574eecbba512.png)
![F(x;\mu,\sigma) = \left[\left(\frac{e^\mu}{x}\right)^{\pi/(\sigma \sqrt{3})} +1\right]^{-1}.](../I/m/456274822de33ada09d28242305be392.png)