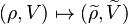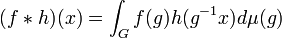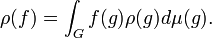Locally profinite group
In mathematics, a locally profinite group is a hausdorff topological group in which every neighborhood of the identity element contains a compact open subgroup. Equivalently, a locally profinite group is a topological group that is hausdorff locally compact and totally disconnected. Moreover, a locally profinite group is compact if and only if it is profinite; this explains the terminology. Basic examples of locally profinite groups are discrete groups and p-adic Lie group. Non-examples are real Lie groups which have no small subgroup property.
In a locally profinite group, a closed subgroup is locally profinite, and every compact subgroup is contained in an open compact subgroup.
Examples
Important examples of locally profinite groups come from algebraic number theory. Let F be a non-archimedean local field. Then both F and 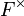 are locally profinite. More generally, the matrix ring
are locally profinite. More generally, the matrix ring 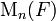 and the general linear group
and the general linear group 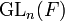 are locally profinite. Another example of a locally profinite group is the absolute Weil group of a non-archimedean local field: this is in contrast to the fact that the absolute Galois group of such is profinite (in particular compact).
are locally profinite. Another example of a locally profinite group is the absolute Weil group of a non-archimedean local field: this is in contrast to the fact that the absolute Galois group of such is profinite (in particular compact).
Representations of a locally profinite group
Let G be a locally profinite group. Then a group homomorphism 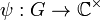 is continuous if and only if it has open kernel.
is continuous if and only if it has open kernel.
Let 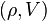 be a complex representation of G.[1]
be a complex representation of G.[1]  is said to be smooth if V is a union of
is said to be smooth if V is a union of 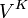 where K runs over all open compact subgroups K.
where K runs over all open compact subgroups K.  is said to be admissible if it is smooth and
is said to be admissible if it is smooth and 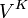 is finite-dimensional for any open compact subgroup K.
is finite-dimensional for any open compact subgroup K.
We now make a blanket assumption that 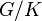 is at most countable for all open compact subgroups K.
is at most countable for all open compact subgroups K.
The dual space 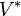 carries the action
carries the action 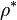 of G given by
of G given by 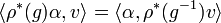 . In general,
. In general, 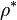 is not smooth. Thus, we set
is not smooth. Thus, we set 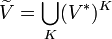 where
where  is acting through
is acting through 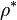 and set
and set 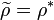 . The smooth representation
. The smooth representation 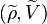 is then called the contragredient or smooth dual of
is then called the contragredient or smooth dual of 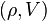 .
.
The contravariant functor
from the category of smooth representations of G to itself is exact. Moreover, the following are equivalent.
-
 is admissible.
is admissible. -
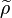 is admissible.[2]
is admissible.[2] - The canonical G-module map
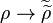 is an isomorphism.
is an isomorphism.
When  is admissible,
is admissible,  is irreducible if and only if
is irreducible if and only if 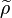 is irreducible.
is irreducible.
The countability assumption at the beginning is really necessary, for there exists a locally profinite group that admits an irreducible smooth representation  such that
such that 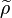 is not irreducible.
is not irreducible.
Hecke algebra of a locally profinite group
- See also: Hecke algebra of a locally compact group
Let  be a unimodular locally profinite group such that
be a unimodular locally profinite group such that 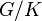 is at most countable for all open compact subgroups K, and
is at most countable for all open compact subgroups K, and  a left Haar measure on
a left Haar measure on  . Let
. Let 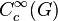 denote the space of locally constant functions on
denote the space of locally constant functions on  with compact support. With the multiplicative structure given by
with compact support. With the multiplicative structure given by
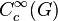 becomes not necessarily unital associative
becomes not necessarily unital associative 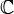 -algebra. It is called the Hecke algebra of G and is denoted by
-algebra. It is called the Hecke algebra of G and is denoted by 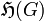 . The algebra plays an important role in the study of smooth representations of locally profinite groups. Indeed, one has the following: given a smooth representation
. The algebra plays an important role in the study of smooth representations of locally profinite groups. Indeed, one has the following: given a smooth representation 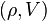 of G, we define a new action on V:
of G, we define a new action on V:
Thus, we have the functor 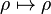 from the category of smooth representations of
from the category of smooth representations of  to the category of non-degenerate
to the category of non-degenerate 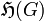 -modules. Here, "non-degenerate" means
-modules. Here, "non-degenerate" means 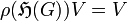 . Then the fact is that the functor is an equivalence.[3]
. Then the fact is that the functor is an equivalence.[3]
Notes
References
- Corinne Blondel, Basic representation theory of reductive p-adic groups
- Bushnell, Colin J.; Henniart, Guy (2006), The local Langlands conjecture for GL(2), Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences] 335, Berlin, New York: Springer-Verlag, doi:10.1007/3-540-31511-X, ISBN 978-3-540-31486-8, MR 2234120
- Milne, J.S. (1988), Canonical models of (mixed) Shimura varieties and automorphic vector bundles, MR 1044823