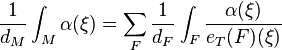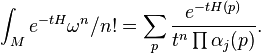Localization formula for equivariant cohomology
In differential geometry, the localization formula states: for an equivariantly closed equivariant differential form  on an orbifold M with a torus action and for a sufficient small
on an orbifold M with a torus action and for a sufficient small 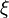 in the Lie algebra of the torus T,
in the Lie algebra of the torus T,
where the sum runs over all connected components F of the set of fixed points 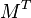 ,
, 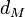 is the orbifold multiplicity of M (which is one if M is a manifold) and
is the orbifold multiplicity of M (which is one if M is a manifold) and 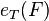 is the equivariant Euler form of the normal bundle of F.
is the equivariant Euler form of the normal bundle of F.
The formula allows one to compute the equivariant cohomogy ring of the orbifold M (a particular kind of differentiable stack) from the equivariant cohomology of its fixed point components, up to multiplicities and Euler forms. No analog of such results holds in the non-equivariant cohomology.
One important consequence of the formula is the Duistermaat–Heckman theorem, which states: supposing there is a Hamiltonian circle action (for simplicity) on a compact symplectic manifold M of dimension 2n,
where H is Hamiltonian for the circle action, the sum is over points fixed by the circle action and 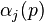 are eigenvalues on the tangent space at p (cf. Lie group action.)
are eigenvalues on the tangent space at p (cf. Lie group action.)
The localization formula can also computes the Fourier transform of (Kostant's symplectic form on) coadjoint orbit, yielding the Harish-Chandra's integration formula, which in turns gives Kirillov's character formula.
The localization theorem for equivariant cohomology in non-rational coefficients is discussed in Quillen's papers.
Non-abelian localization
The localization theorem states that the equivariant cohomology can be recovered, up to torsion elements, from the equivariant cohomology of the fixed point subset. This does not extend, in verbatim, to the non-abelian action. But there is still a version of the localization theorem for non-abelian actions.
References
- M. Atiyah, R. Bott, The moment map and equivariant cohomology, Topology 23 (1984).
- Liu, Kefeng (2006), "Localization and conjectures from string duality", in Ge, Mo-Lin; Zhang, Weiping, Differential geometry and physics, Nankai Tracts in Mathematics 10, World Scientific, pp. 63–105, ISBN 978-981-270-377-4, MR 2322389
- E. Meinrenken.; Symplectic surgery and the Spin-c Dirac operator. Advances in Mathematics 134 (1998), 240–277
- D. Quillen, The spectrum of an equivariant cohomology ring, I, II