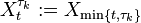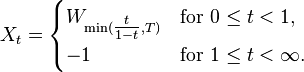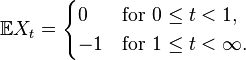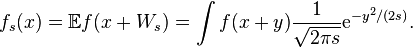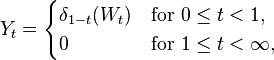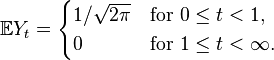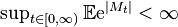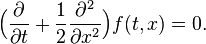Local martingale

In mathematics, a local martingale is a type of stochastic process, satisfying the localized version of the martingale property. Every martingale is a local martingale; every bounded local martingale is a martingale; in particular, every local martingale that is bounded from below is a supermartingale, and every local martingale that is bounded from above is a submartingale; however, in general a local martingale is not a martingale, because its expectation can be distorted by large values of small probability. In particular, a driftless diffusion process is a local martingale, but not necessarily a martingale.

Local martingales are essential in stochastic analysis, see Itō calculus, semimartingale, Girsanov theorem.

Definition

Let (Ω, F, P) be a probability space; let F_∗ = { F_t | t ≥ 0 } be a filtration of F; let X : [0, +∞) × Ω → S be an F_∗-adapted stochastic process on set S. Then X is called an F_∗-local martingale if there exists a sequence of F_∗-stopping times τ_k : Ω → [0, +∞) such that

the τ_k are almost surely increasing: P[τ_k < τ_k+1] = 1;
the τ_k diverge almost surely: P[τ_k → +∞ as k → +∞] = 1;
the stopped process

X_t^{\tau_{k}} := X_{\min \{ t, \tau_k \}}

is an F_∗-martingale for every k.

Examples

Example 1

Let W_t be the Wiener process and T = min{ t : W_t = −1 } the time of first hit of −1. The stopped process W_{min{ t, T }} is a martingale; its expectation is 0 at all times, nevertheless its limit (as t → ∞) is equal to −1 almost surely (a kind of gambler's ruin). A time change leads to a process

\displaystyle X_t = \begin{cases} W_{\min(\tfrac{t}{1-t},T)} &\text{for } 0 \le t < 1,\\ -1 &\text{for } 1 \le t < \infty. \end{cases}

The process 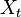$X_t$ is continuous almost surely; nevertheless, its expectation is discontinuous,

\displaystyle \mathbb{E} X_t = \begin{cases} 0 &\text{for } 0 \le t < 1,\\ -1 &\text{for } 1 \le t < \infty. \end{cases}

This process is not a martingale. However, it is a local martingale. A localizing sequence may be chosen as 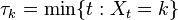$\tau_k = \min \{ t : X_t = k \}$ if there is such t, otherwise τ_k = k. This sequence diverges almost surely, since τ_k = k for all k large enough (namely, for all k that exceed the maximal value of the process X). The process stopped at τ_k is a martingale.^{[details 1]}

Example 2

Let W_t be the Wiener process and ƒ a measurable function such that 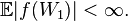$\mathbb{E} |f(W_1)| < \infty.$ Then the following process is a martingale:

\displaystyle X_t = \mathbb{E} ( f(W_1) | F_t ) = \begin{cases} f_{1-t}(W_t) &\text{for } 0 \le t < 1,\\ f(W_1) &\text{for } 1 \le t < \infty; \end{cases}

here

\displaystyle f_s(x) = \mathbb{E} f(x+W_s) = \int f(x+y) \frac1{\sqrt{2\pi s}} \mathrm{e}^{-y^2/(2s)} .

The Dirac delta function 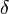$\delta$ (strictly speaking, not a function), being used in place of 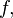$f,$ leads to a process defined informally as 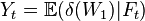$Y_t = \mathbb{E} ( \delta(W_1) | F_t )$ and formally as

\displaystyle Y_t = \begin{cases} \delta_{1-t}(W_t) &\text{for } 0 \le t < 1,\\ 0 &\text{for } 1 \le t < \infty, \end{cases}

where

\displaystyle \delta_s(x) = \frac1{\sqrt{2\pi s}} \mathrm{e}^{-x^2/(2s)} .

The process 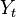$Y_t$ is continuous almost surely (since 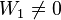$W_1 \ne 0$ almost surely), nevertheless, its expectation is discontinuous,

\displaystyle \mathbb{E} Y_t = \begin{cases} 1/\sqrt{2\pi} &\text{for } 0 \le t < 1,\\ 0 &\text{for } 1 \le t < \infty. \end{cases}

This process is not a martingale. However, it is a local martingale. A localizing sequence may be chosen as 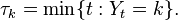$\tau_k = \min \{ t : Y_t = k \}.$

Example 3

Let 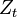$Z_t$ be the complex-valued Wiener process, and

\displaystyle X_t = \ln | Z_t - 1 | \, .

The process 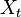$X_t$ is continuous almost surely (since 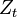$Z_t$ does not hit 1, almost surely), and is a local martingale, since the function 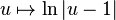$u \mapsto \ln|u-1|$ is harmonic (on the complex plane without the point 1). A localizing sequence may be chosen as 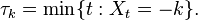$\tau_k = \min \{ t : X_t = -k \}.$ Nevertheless, the expectation of this process is non-constant; moreover,

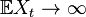\displaystyle \mathbb{E} X_t \to \infty

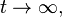
t \to \infty,

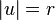which can be deduced from the fact that the mean value of $\ln|u-1|$ over the circle $|u|=r$ tends to infinity as 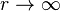$r \to \infty$ . (In fact, it is equal to 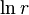$\ln r$ for r ≥ 1 but to 0 for r ≤ 1).

Martingales via local martingales

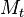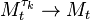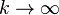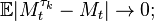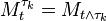Let $M_t$ be a local martingale. In order to prove that it is a martingale it is sufficient to prove that $M_t^{\tau_k} \to M_t$ in L¹ (as $k \to \infty$ ) for every t, that is, $\mathbb{E} | M_t^{\tau_k} - M_t | \to 0;$ here $M_t^{\tau_k} = M_{t\wedge \tau_k}$ is the stopped process. The given relation 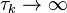$\tau_k \to \infty$ implies that 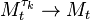$M_t^{\tau_k} \to M_t$ almost surely. The dominated convergence theorem ensures the convergence in L¹ provided that

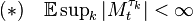\textstyle (*) \quad \mathbb{E} \sup_k| M_t^{\tau_k} | < \infty

for every t.

Thus, Condition (*) is sufficient for a local martingale 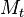$M_t$ being a martingale. A stronger condition

\textstyle (**) \quad \mathbb{E} \sup_{s\in[0,t]} |M_s| < \infty

for every t

is also sufficient.

Caution. The weaker condition

\textstyle \sup_{s\in[0,t]} \mathbb{E} |M_s| < \infty

for every t

is not sufficient. Moreover, the condition

\textstyle \sup_{t\in[0,\infty)} \mathbb{E} \mathrm{e}^{|M_t|} < \infty

is still not sufficient; for a counterexample see Example 3 above.

A special case:

\textstyle M_t = f(t,W_t),

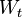where $W_t$ is the Wiener process, and 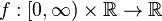$f : [0,\infty) \times \mathbb{R} \to \mathbb{R}$ is twice continuously differentiable. The process 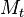$M_t$ is a local martingale if and only if f satisfies the PDE

\Big( \frac{\partial}{\partial t} + \frac12 \frac{\partial^2}{\partial x^2} \Big) f(t,x) = 0.

However, this PDE itself does not ensure that 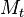$M_t$ is a martingale. In order to apply (**) the following condition on f is sufficient: for every 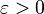$\varepsilon>0$ and t there exists 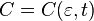$C = C(\varepsilon,t)$ such that

\textstyle |f(s,x)| \le C \mathrm{e}^{\varepsilon x^2}

for all $s \in [0,t]$ and $x \in \mathbb{R}.$

Technical details

↑ For the times before 1 it is a martingale since a stopped Brownian motion is. After the instant 1 it is constant. It remains to check it at the instant 1. By the bounded convergence theorem the expectation at 1 is the limit of the expectation at (n-1)/n (as n tends to infinity), and the latter does not depend on n. The same argument applies to the conditional expectation.

References

Øksendal, Bernt K. (2003). Stochastic Differential Equations: An Introduction with Applications (Sixth edition ed.). Berlin: Springer. ISBN 3-540-04758-1.

Stochastic processes

Discrete time	Bernoulli process Branching process Chinese restaurant process Galton–Watson process Independent and identically distributed random variables Markov chain Moran process Random walk Loop-erased Self-avoiding

Continuous time	Bessel process Birth–death process Brownian motion Bridge Excursion Fractional Geometric Meander Cauchy process Contact process Continuous-time random walk Cox process Diffusion process Empirical process Feller process Fleming–Viot process Gamma process Hunt process Interacting particle systems Itō diffusion Itō process Jump diffusion Jump process Lévy process Local time Markov additive process McKean–Vlasov process Ornstein–Uhlenbeck process Poisson process Compound Non-homogeneous Point process Schramm–Loewner evolution Semimartingale Sigma-martingale Stable process Superprocess Telegraph process Variance gamma process Wiener process Wiener sausage

Both	Branching process Gaussian process Hidden Markov model (HMM) Markov process Martingale Differences Local Sub- Super- Random dynamical system Regenerative process Renewal process White noise

Fields and other	Dirichlet process Gaussian random field Gibbs measure Hopfield model Ising model Potts model Boolean network Markov random field Percolation Pitman–Yor process Point process Cox Poisson Random field Random graph

Time series models	Autoregressive conditional heteroskedasticity (ARCH) model Autoregressive integrated moving average (ARIMA) model Autoregressive (AR) model Autoregressive–moving-average (ARMA) model Generalized autoregressive conditional heteroskedasticity (GARCH) model Moving-average (MA) model

Financial models	Black–Derman–Toy Black–Karasinski Black–Scholes Chen Constant elasticity of variance (CEV) Cox–Ingersoll–Ross (CIR) Garman–Kohlhagen Heath–Jarrow–Morton (HJM) Heston Ho–Lee Hull–White LIBOR market SABR volatility Vašíček

Actuarial models	Bühlmann Cramér–Lundberg Risk process Sparre–Anderson

Queueing models	Bulk Fluid Generalized queueing network M/G/1 M/M/1 M/M/c

Properties	Càdlàg paths Continuous Continuous paths Ergodic Exchangeable Feller-continuous Gauss–Markov Markov Mixing Piecewise deterministic Predictable Progressively measurable Self-similar Stationary Time-reversible

Limit theorems	Central limit theorem Donsker's theorem Doob's martingale convergence theorems Ergodic theorem Fisher–Tippett–Gnedenko theorem Large deviation principle Law of large numbers (weak/strong) Law of the iterated logarithm Maximal ergodic theorem Sanov's theorem

Inequalities	Burkholder–Davis–Gundy Doob's martingale Kunita–Watanabe

Tools	Cameron–Martin formula Convergence of random variables Doléans-Dade exponential Doob decomposition theorem Doob–Meyer decomposition theorem Doob's optional stopping theorem Dynkin's formula Feynman–Kac formula Filtration Girsanov theorem Infinitesimal generator Itō integral Itō's lemma Kolmogorov continuity theorem Kolmogorov extension theorem Lévy–Prokhorov metric Malliavin calculus Martingale representation theorem Optional stopping theorem Prohorov theorem Quadratic variation Reflection principle Skorokhod integral Skorokhod's representation theorem Skorokhod space Snell envelope Stochastic differential equation Tanaka Stopping time Stratonovich integral Uniform integrability Usual hypotheses Wiener space Classical Abstract

Disciplines	Actuarial mathematics Econometrics Ergodic theory Extreme value theory (EVT) Large deviations theory Mathematical finance Mathematical statistics Probability theory Queueing theory Renewal theory Ruin theory Statistics Stochastic analysis Time series analysis Machine learning

List of topics Category