Local flatness

In topology, a branch of mathematics, local flatness is a property of a submanifold in a topological manifold of larger dimension. In the category of topological manifolds, locally flat submanifolds play a role similar to that of embedded submanifolds in the category of smooth manifolds.

Suppose a d dimensional manifold N is embedded into an n dimensional manifold M (where d < n). If 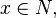x \in N, we say N is locally flat at x if there is a neighborhood 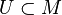U \subset M of x such that the topological pair 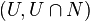(U, U\cap N) is homeomorphic to the pair 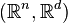(\mathbb{R}^n,\mathbb{R}^d), with a standard inclusion of 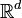\mathbb{R}^d as a subspace of 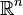\mathbb{R}^n. 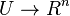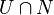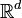That is, there exists a homeomorphism U\to R^n such that the image of U\cap N coincides with \mathbb{R}^d.

The above definition assumes that, if M has a boundary, x is not a boundary point of M. If x is a point on the boundary of M then the definition is modified as follows. We say that N is locally flat at a boundary point x of M if there is a neighborhood 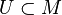U\subset M of x such that the topological pair 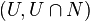(U, U\cap N) is homeomorphic to the pair 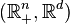(\mathbb{R}^n_+,\mathbb{R}^d), where 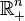\mathbb{R}^n_+ is a standard half-space and 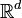\mathbb{R}^d is included as a standard subspace of its boundary. 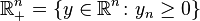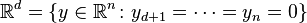In more detail, we can set \mathbb{R}^n_+ = \{y \in \mathbb{R}^n\colon y_n \ge 0\} and \mathbb{R}^d = \{y \in \mathbb{R}^n\colon y_{d+1}=\cdots=y_n=0\}.

We call N locally flat in M if N is locally flat at every point. Similarly, a map 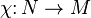\chi\colon N\to M is called locally flat, even if it is not an embedding, if every x in N has a neighborhood U whose image 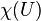\chi(U) is locally flat in M.

Local flatness of an embedding implies strong properties not shared by all embeddings. Brown (1962) proved that if d = n − 1, then N is collared; that is, it has a neighborhood which is homeomorphic to N × [0,1] with N itself corresponding to N × 1/2 (if N is in the interior of M) or N × 0 (if N is in the boundary of M).

See also

References