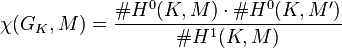Local Euler characteristic formula
In the mathematical field of Galois cohomology, the local Euler characteristic formula is a result due to John Tate that computes the Euler characteristic of the group cohomology of the absolute Galois group GK of a non-archimedean local field K.
Statement
Let K be a non-archimedean local field, let Ks denote a separable closure of K, let GK = Gal(Ks/K) be the absolute Galois group of K, and let Hi(K, M) denote the group cohomology of GK with coefficients in M. Since the cohomological dimension of GK is two,[1] Hi(K, M) = 0 for i ≥ 3. Therefore, the Euler characteristic only involves the groups with i = 0, 1, 2.
Case of finite modules
Let M be a GK-module of finite order m. The Euler characteristic of M is defined to be[2]
(the ith cohomology groups for i ≥ 3 appear tacitly as their sizes are all one).
Let R denote the ring of integers of K. Tate's result then states that if m is relatively prime to the characteristic of K, then[3]
i.e. the inverse of the order of the quotient ring R/mR.
Two special cases worth singling out are the following. If the order of M is relatively prime to the characteristic of the residue field of K, then the Euler characteristic is one. If K is a finite extension of the p-adic numbers Qp, and if vp denotes the p-adic valuation, then
where [K:Qp] is the degree of K over Qp.
The Euler characteristic can be rewritten, using local Tate duality, as
where M′ is the local Tate dual of M.
Notes
- ↑ Serre 2002, §II.4.3
- ↑ The Euler characteristic in a cohomology theory is normally written as an alternating sum of the sizes of the cohomology groups. In this case, the alternating product is more standard.
- ↑ Milne 2006, Theorem I.2.8
References
- Milne, James S. (2006), Arithmetic duality theorems (second ed.), Charleston, SC: BookSurge, LLC, ISBN 1-4196-4274-X, MR 2261462, retrieved 2010-03-27
- Serre, Jean-Pierre (2002), Galois cohomology, Springer Monographs in Mathematics, Berlin, New York: Springer-Verlag, ISBN 978-3-540-42192-4, MR 1867431, translation of Cohomologie Galoisienne, Springer-Verlag Lecture Notes 5 (1964).
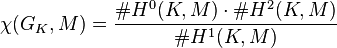
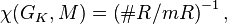
![\chi(G_K,M)=p^{-[K:\mathbf{Q}_p]v_p(m)}](../I/m/356b554739d8efc1df8954bae1e0fac3.png)