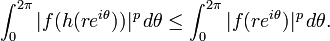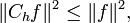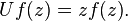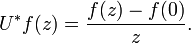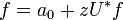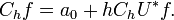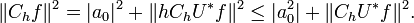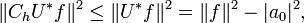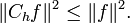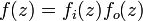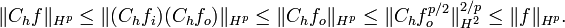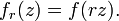Littlewood subordination theorem
In mathematics, the Littlewood subordination theorem, proved by J. E. Littlewood in 1925, is a theorem in operator theory and complex analysis. It states that any holomorphic univalent self-mapping of the unit disk in the complex numbers that fixes 0 induces a contractive composition operator on various function spaces of holomorphic functions on the disk. These spaces include the Hardy spaces, the Bergman spaces and Dirichlet space.
Subordination theorem
Let h be a holomorphic univalent mapping of the unit disk D into itself such that h(0) = 0. Then the composition operator Ch defined on holomorphic functions f on D by
defines a linear operator with operator norm less than 1 on the Hardy spaces 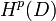 , the Bergman spaces
, the Bergman spaces 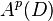 .
(1 ≤ p < ∞) and the Dirichlet space
.
(1 ≤ p < ∞) and the Dirichlet space 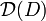 .
.
The norms on these spaces are defined by:
Littlewood's inequalities
Let f be a holomorphic function on the unit disk D and let h be a holomorphic univalent mapping of D into itself with h(0) = 0. Then if 0 < r < 1 and 1 ≤ p < ∞
This inequality also holds for 0 < p < 1, although in this case there is no operator interpretation.
Proofs
Case p = 2
To prove the result for H2 it suffices to show that for f a polynomial[1]
Let U be the unilateral shift defined by
This has adjoint U* given by
Since f(0) = a0, this gives
and hence
Thus
Since U*f has degree less than f, it follows by induction that
and hence
The same method of proof works for A2 and 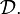
General Hardy spaces
If f is in Hardy space Hp, then it has a factorization[2]
with fi an inner function and fo an outer function.
Then
Inequalities
Taking 0 < r < 1, Littlewood's inequalities follow by applying the Hardy space inequalities to the function
The inequalities can also be deduced, following Riesz (1925), using subharmonic functions.[3][4] The inequaties in turn immediately imply the subordination theorem for general Bergman spaces.
Notes
- ↑ Nikolski 2002, pp. 56–57
- ↑ Nikolski 2002, p. 57
- ↑ Duren 1970
- ↑ Shapiro 1993, p. 19
References
- Duren, P. L. (1970), Theory of H p spaces, Pure and Applied Mathematics 38, Academic Press
- Littlewood, J. E. (1925), "On inequalities in the theory of functions", Proc. London Math. Soc. 23: 481–519
- Nikolski, N. K. (2002), Operators, functions, and systems: an easy reading. Vol. 1. Hardy, Hankel, and Toeplitz, Mathematical Surveys and Monographs 92, American Mathematical Society, ISBN 0-8218-1083-9
- Riesz, F. (1925), "Sur une inégalite de M. Littlewood dans la théorie des fonctions", Proc. London Math. Soc. 23: 36–39
- Shapiro, J. H. (1993), Composition operators and classical function theory, Universitext: Tracts in Mathematics, Springer-Verlag, ISBN 0-387-94067-7