List of mathematical symbols
- This list is incomplete; you can help by expanding it.
This is a list of symbols found within all branches of mathematics to express a formula or to represent a constant.
When reading the list, it is important to recognize that a mathematical concept is independent of the symbol chosen to represent it. For many of the symbols below, the symbol is usually synonymous with the corresponding concept (ultimately an arbitrary choice made as a result of the cumulative history of mathematics), but in some situations a different convention may be used. For example, depending on context, the triple bar "≡" may represent congruence or a definition. Further, in mathematical logic, numerical equality is sometimes represented by "≡" instead of "=", with the latter representing equality of well-formed formulas. In short, convention dictates the meaning.
Each symbol is shown both in HTML, whose display depends on the browser's access to an appropriate font installed on the particular device, and in TeX, as an image.
Guide
This list is organized by symbol type and is intended to facilitate finding an unfamiliar symbol by its visual appearance. For a related list organized by mathematical topic, see List of mathematical symbols by subject. That list also includes LaTeX and HTML markup and Unicode code points for each symbol.
- Basic symbols: Symbols widely used in mathematics, roughly through first-year calculus. More advanced meanings are included with some symbols listed here.
- Symbols based on equality "=": Symbols derived from or similar to the equal sign, including double-headed arrows. Not surprisingly these symbols are often associated with an equivalence relation.
- Symbols that point left or right: Symbols, such as < and >, that appear to point to one side or another.
- Brackets: Symbols that are placed on either side of a variable or expression, such as |x|.
- Other non-letter symbols: Symbols that do not fall in any of the other categories.
- Letter-based symbols: Many mathematical symbols are based on, or closely resemble, a letter in some alphabet. This section includes such symbols, including symbols that resemble upside-down letters. Many letters have conventional meanings in various branches of mathematics and physics. These are not listed here. The See also section, below, has several lists of such usages.
- Letter modifiers: Symbols that can be placed on or next to any letter to modify the letter's meaning.
- Symbols based on Latin letters, including those symbols that resemble or contain an X
- Symbols based on Hebrew or Greek letters e.g. ב ,א, δ, Δ, π, Π, σ, Σ, Φ. Note: symbols resembling Λ are grouped with "V" under Latin letters.
- Variations: Usage in languages written right-to-left
Basic symbols
| Symbol in HTML |
Symbol in TeX |
Name | Explanation | Examples |
|---|---|---|---|---|
| Read as | ||||
| Category | ||||
+ |
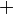 |
plus;
add |
4 + 6 means the sum of 4 and 6. | 2 + 7 = 9 |
|
the disjoint union of ... and ...
|
A1 + A2 means the disjoint union of sets A1 and A2. | A1 = {3, 4, 5, 6} ∧ A2 = {7, 8, 9, 10} ⇒ A1 + A2 = {(3,1), (4,1), (5,1), (6,1), (7,2), (8,2), (9,2), (10,2)} | ||
− |
 |
9 − 4 means the subtraction of 4 from 9. | 8 − 3 = 5 | |
|
negative;
minus; the opposite of |
−3 means the negative of the number 3. | −(−5) = 5 | ||
|
minus;
without |
A − B means the set that contains all the elements of A that are not in B. (∖ can also be used for set-theoretic complement as described below.) |
{1,2,4} − {1,3,4} = {2} | ||
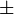 |
plus or minus
|
6 ± 3 means both 6 + 3 and 6 − 3. | The equation x = 5 ± √4, has two solutions, x = 7 and x = 3. | |
|
plus or minus
|
10 ± 2 or equivalently 10 ± 20% means the range from 10 − 2 to 10 + 2. | If a = 100 ± 1 mm, then a ≥ 99 mm and a ≤ 101 mm. | ||
∓ |
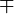 |
minus-plus
minus or plus
|
6 ± (3 ∓ 5) means 6 + (3 − 5) and 6 − (3 + 5). | cos(x ± y) = cos(x) cos(y) ∓ sin(x) sin(y). |
  |
times;
multiplied by |
3 × 4 or 3 · 4 means the multiplication of 3 by 4. | 7 · 8 = 56 | |
|
dot
|
u · v means the dot product of vectors u and v | (1,2,5) · (3,4,−1) = 6 | ||
|
placeholder
(silent)
|
A · means a placeholder for an argument of a function. Indicates the functional nature of an expression without assigning a specific symbol for an argument. |  | ||
÷ ⁄ |
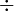 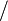 |
divided by;
over |
6 ÷ 3 or 6 ⁄ 3 means the division of 6 by 3. | 2 ÷ 4 = 0.5 12 ⁄ 4 = 3 |
|
mod
|
G / H means the quotient of group G modulo its subgroup H. | {0, a, 2a, b, b+a, b+2a} / {0, b} = {{0, b}, {a, b+a}, {2a, b+2a}} | ||
|
quotient set
mod
|
A/~ means the set of all ~ equivalence classes in A. | If we define ~ by x ~ y ⇔ x − y ∈ ℤ, then ℝ/~ = { {x + n : n ∈ ℤ } : x ∈ [0,1) } | ||
√ |
 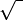 |
the (principal) square root of
real numbers |
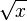 means the nonnegative number whose square is means the nonnegative number whose square is  . . |
 |
|
the (complex) square root of
complex numbers |
if 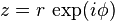 is represented in polar coordinates with is represented in polar coordinates with  , then , then 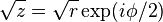 . . |
 | ||
∑ |
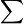 |
sum over ... from ... to ... of
|
 means means  . . |
 |
 |
indefinite integral or antiderivative
indefinite integral of
the antiderivative of |
∫ f(x) dx means a function whose derivative is f. |
∫ x2 dx = x3/3 + C | |
|
definite integral
integral from ... to ... of ... with respect to
|
∫b a f(x) dx means the signed area between the x-axis and the graph of the function f between x = a and x = b. |
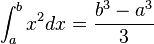 | ||
|
line/ path/ curve/ integral of ... along ...
|
∫ C f ds means the integral of f along the curve C, 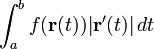 , where r is a parametrization of C. (If the curve is closed, the symbol ∮ , where r is a parametrization of C. (If the curve is closed, the symbol ∮may be used instead, as described below.) |
|||
∮ |
 |
Contour integral;
closed line integral contour integral of
|
Similar to the integral, but used to denote a single integration over a closed curve or loop. It is sometimes used in physics texts involving equations regarding Gauss's Law, and while these formulas involve a closed surface integral, the representations describe only the first integration of the volume over the enclosing surface. Instances where the latter requires simultaneous double integration, the symbol ∯ would be more appropriate. A third related symbol is the closed volume integral, denoted by the symbol ∰ . The contour integral can also frequently be found with a subscript capital letter C, ∮ |
If C is a Jordan curve about 0, then 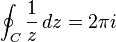 . . |
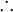 |
therefore
therefore;
so; hence everywhere |
Sometimes used in proofs before logical consequences. | All humans are mortal. Socrates is a human. ∴ Socrates is mortal. | |
∵ |
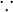 |
because;
since everywhere |
Sometimes used in proofs before reasoning. | 11 is prime ∵ it has no positive integer factors other than itself and one. |
 |
factorial
|
n! means the product 1 × 2 × ... × n. | 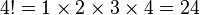 | |
|
logical negation
not
propositional logic |
The statement !A is true if and only if A is false. A slash placed through another operator is the same as "!" placed in front. (The symbol ! is primarily from computer science. It is avoided in mathematical texts, where the notation ¬A is preferred.) |
!(!A) ⇔ A x ≠ y ⇔ !(x = y) | ||
¬ ˜ |
 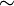 |
logical negation
not
propositional logic |
The statement ¬A is true if and only if A is false. A slash placed through another operator is the same as "¬" placed in front. (The symbol ~ has many other uses, so ¬ or the slash notation is preferred. Computer scientists will often use ! but this is avoided in mathematical texts.) |
¬(¬A) ⇔ A x ≠ y ⇔ ¬(x = y) |
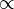 |
is proportional to;
varies as everywhere |
y ∝ x means that y = kx for some constant k. | if y = 2x, then y ∝ x. | |
 |
infinity
|
∞ is an element of the extended number line that is greater than all real numbers; it often occurs in limits. | 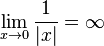 | |
   |
end of proof
everywhere |
Used to mark the end of a proof. (May also be written Q.E.D.) |
Symbols based on equality sign
| Symbol in HTML |
Symbol in TeX |
Name | Explanation | Examples |
|---|---|---|---|---|
| Read as | ||||
| Category | ||||
 |
is equal to;
equals everywhere |
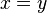 means means  and and  represent the same math object (Both symbols have the same value). represent the same math object (Both symbols have the same value). |
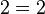  | |
≠ |
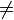 |
is not equal to;
does not equal everywhere |
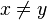 means that means that  and and  do not represent the same math object (Both symbols do not have the same value). do not represent the same math object (Both symbols do not have the same value).(The forms !=, /= or <> are generally used in programming languages where ease of typing and use of ASCII text is preferred.) |
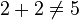 |
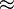 |
approximately equal
is approximately equal to
everywhere |
x ≈ y means x is approximately equal to y. This may also be written ≃, ≅, ~, ♎ (Libra Symbol), or ≒. |
π ≈ 3.14159 | |
|
is isomorphic to
|
G ≈ H means that group G is isomorphic (structurally identical) to group H. (≅ can also be used for isomorphic, as described below.) |
Q8 / C2 ≈ V | ||
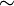 |
has distribution
|
X ~ D, means the random variable X has the probability distribution D. | X ~ N(0,1), the standard normal distribution | |
|
row equivalence
is row equivalent to
|
A ~ B means that B can be generated by using a series of elementary row operations on A |  | ||
|
same order of magnitude
roughly similar;
poorly approximates |
m ~ n means the quantities m and n have the same order of magnitude, or general size. (Note that ~ is used for an approximation that is poor, otherwise use ≈ .) |
2 ~ 5 8 × 9 ~100 but π2 ≈ 10 | ||
|
is similar to[1]
|
△ABC ~ △DEF means triangle ABC is similar to (has the same shape) triangle DEF. | |||
|
is asymptotically equivalent to
|
f ~ g means 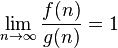 . . |
x ~ x+1 | ||
|
are in the same equivalence class
everywhere |
a ~ b means ![b \in [a]](../I/m/6769b7a159bc917be1478849db21b7ae.png) (and equivalently (and equivalently ![a \in [b]](../I/m/3ec8d0d70da247252e9aa1380a011f27.png) ). ). |
1 ~ 5 mod 4 | ||
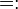 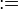  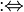 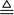 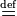  |
is defined as;
is equal by definition to everywhere |
x := y, y =: x or x ≡ y means x is defined to be another name for y, under certain assumptions taken in context. (Some writers use ≡ to mean congruence). P :⇔ Q means P is defined to be logically equivalent to Q. |
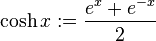 | |
≅ |
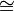 |
is congruent to
|
△ABC ≅ △DEF means triangle ABC is congruent to (has the same measurements as) triangle DEF. | |
|
isomorphic
is isomorphic to
|
G ≅ H means that group G is isomorphic (structurally identical) to group H. (≈ can also be used for isomorphic, as described above.) |
V ≅ C2 × C2 | ||
 |
... is congruent to ... modulo ...
|
a ≡ b (mod n) means a − b is divisible by n | 5 ≡ 2 (mod 3) | |
⇔ ↔ |
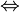 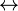 |
material equivalence
if and only if;
iff propositional logic |
A ⇔ B means A is true if B is true and A is false if B is false. | x + 5 = y + 2 ⇔ x + 3 = y |
Symbols that point left or right
| Symbol in HTML |
Symbol in TeX |
Name | Explanation | Examples |
|---|---|---|---|---|
| Read as | ||||
| Category | ||||
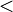 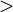 |
is less than,
is greater than |
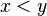 means means  is less than is less than  . .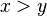 means means  is greater than is greater than  . . |
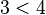  | |
|
proper subgroup
is a proper subgroup of
|
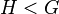 means means  is a proper subgroup of is a proper subgroup of  . . |
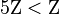 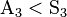 | ||
≪ ≫ |
 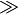 |
significant (strict) inequality
is much less than,
is much greater than |
x ≪ y means x is much less than y. x ≫ y means x is much greater than y. |
0.003 ≪ 1000000 |
|
asymptotic comparison
is of smaller order than,
is of greater order than |
f ≪ g means the growth of f is asymptotically bounded by g. (This is I. M. Vinogradov's notation. Another notation is the Big O notation, which looks like f = O(g).) |
x ≪ ex | ||
≤ ≥ |
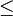 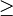 |
is less than or equal to,
is greater than or equal to |
x ≤ y means x is less than or equal to y. x ≥ y means x is greater than or equal to y. (The forms <= and >= are generally used in programming languages, where ease of typing and use of ASCII text is preferred.) |
3 ≤ 4 and 5 ≤ 5 5 ≥ 4 and 5 ≥ 5 |
|
is a subgroup of
|
H ≤ G means H is a subgroup of G. | Z ≤ Z A3 ≤ S3 | ||
|
is reducible to
|
A ≤ B means the problem A can be reduced to the problem B. Subscripts can be added to the ≤ to indicate what kind of reduction. | If
then | ||
≦ ≧ |
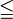 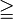 |
... is less than ... is greater than ...
|
7k ≡ 28 (mod 2) is only true if k is an even integer. Assume that the problem requires k to be non-negative; the domain is defined as 0 ≦ k ≦ ∞. | 10a ≡ 5 (mod 5) for 1 ≦ a ≦ 10 |
|
... is less than or equal... is greater than or equal...
|
x ≦ y means that each component of vector x is less than or equal to each corresponding component of vector y. x ≧ y means that each component of vector x is greater than or equal to each corresponding component of vector y. It is important to note that x ≦ y remains true if every element is equal. However, if the operator is changed, x ≤ y is true if and only if x ≠ y is also true. |
|||
≺ ≻ |
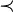 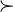 |
Karp reduction
is Karp reducible to;
is polynomial-time many-one reducible to |
L1 ≺ L2 means that the problem L1 is Karp reducible to L2.[2] | If L1 ≺ L2 and L2 ∈ P, then L1 ∈ P. |
|
Nondominated order
is nondominated by
|
P ≺ Q means that the element P is nondominated by element Q.[3] | If P1 ≺ Q2 then  | ||
◅ ▻ |
 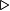 |
is a normal subgroup of
|
N ◅ G means that N is a normal subgroup of group G. | Z(G) ◅ G |
|
ideal
is an ideal of
|
I ◅ R means that I is an ideal of ring R. | (2) ◅ Z | ||
|
antijoin
the antijoin of
|
R ▻ S means the antijoin of the relations R and S, the tuples in R for which there is not a tuple in S that is equal on their common attribute names. | R 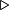 S = R - R S = R - R  S S | ||
⇒ → ⊃ |
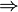  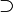 |
implies;
if ... then propositional logic, Heyting algebra |
A ⇒ B means if A is true then B is also true; if A is false then nothing is said about B. (→ may mean the same as ⇒, or it may have the meaning for functions given below.) (⊃ may mean the same as ⇒,[4] or it may have the meaning for superset given below.) |
x = 2 ⇒ x2 = 4 is true, but x2 = 4 ⇒ x = 2 is in general false (since x could be −2). |
⊆ ⊂ |
 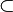 |
is a subset of
|
(subset) A ⊆ B means every element of A is also an element of B.[5] (proper subset) A ⊂ B means A ⊆ B but A ≠ B. (Some writers use the symbol ⊂ as if it were the same as ⊆.) |
(A ∩ B) ⊆ A ℕ ⊂ ℚ ℚ ⊂ ℝ |
⊇ ⊃ |
 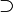 |
superset
is a superset of
|
A ⊇ B means every element of B is also an element of A. A ⊃ B means A ⊇ B but A ≠ B. (Some writers use the symbol ⊃ as if it were the same as ⊇.) |
(A ∪ B) ⊇ B ℝ ⊃ ℚ |
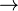 |
function arrow
from ... to
|
f: X → Y means the function f maps the set X into the set Y. | Let f: ℤ → ℕ ∪ {0} be defined by f(x) := x2. | |
↦ |
 |
function arrow
maps to
|
f: a ↦ b means the function f maps the element a to the element b. | Let f: x ↦ x + 1 (the successor function). |
<: <· |
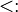 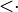 |
subtype
is a subtype of
|
T1 <: T2 means that T1 is a subtype of T2. | If S <: T and T <: U then S <: U (transitivity). |
|
is covered by
|
x <• y means that x is covered by y. | {1, 8} <• {1, 3, 8} among the subsets of {1, 2, ..., 10} ordered by containment. | ||
⊧ |
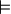 |
entailment
entails
|
A ⊧ B means the sentence A entails the sentence B, that is in every model in which A is true, B is also true. | A ⊧ A ∨ ¬A |
⊢ |
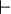 |
infers;
is derived from propositional logic, predicate logic |
x ⊢ y means y is derivable from x. | A → B ⊢ ¬B → ¬A |
|
is a partition of
|
p ⊢ n means that p is a partition of n. | (4,3,1,1) ⊢ 9,  | ||
⟨| |
 |
bra vector
the bra ...;
the dual of ... Dirac notation |
⟨φ| means the dual of the vector |φ⟩, a linear functional which maps a ket |ψ⟩ onto the inner product ⟨φ|ψ⟩. | |
|⟩ |
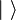 |
ket vector
the ket ...;
the vector ... Dirac notation |
|φ⟩ means the vector with label φ, which is in a Hilbert space. | A qubit's state can be represented as α|0⟩+ β|1⟩, where α and β are complex numbers s.t. |α|2 + |β|2 = 1. |
Brackets
| Symbol in HTML |
Symbol in TeX |
Name | Explanation | Examples |
|---|---|---|---|---|
| Read as | ||||
| Category | ||||
 |
n choose k
|
 means (in the case of n = positive integer) the number of combinations of k elements drawn from a set of n elements. (This may also be written as C(n, k), C(n; k), nCk, nCk, or 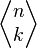 .) .) |

| |
 |
multiset coefficient
u multichoose k
|
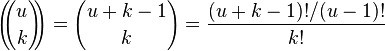 (when u is positive integer) means reverse or rising binomial coefficient. |
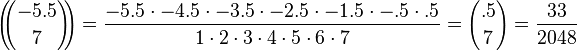 | |
|...| |
 |
absolute value;
modulus absolute value of; modulus of
|
|x| means the distance along the real line (or across the complex plane) between x and zero. | |3| = 3 |–5| = |5| = 5 | i | = 1 | 3 + 4i | = 5 |
|
Euclidean norm or Euclidean length or magnitude
Euclidean norm of
|
|x| means the (Euclidean) length of vector x. | For x = (3,−4) 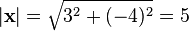 | ||
|
determinant of
|
|A| means the determinant of the matrix A | 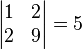 | ||
|
cardinality of;
size of; order of |
|X| means the cardinality of the set X. (# may be used instead as described below.) |
|{3, 5, 7, 9}| = 4. | ||
‖...‖ |
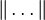 |
norm of;
length of |
‖ x ‖ means the norm of the element x of a normed vector space.[6] | ‖ x + y ‖ ≤ ‖ x ‖ + ‖ y ‖ |
|
nearest integer to
|
‖x‖ means the nearest integer to x. (This may also be written [x], ⌊x⌉, nint(x) or Round(x).) |
‖1‖ = 1, ‖1.6‖ = 2, ‖−2.4‖ = −2, ‖3.49‖ = 3 | ||
{ , } |
 |
set brackets
the set of ...
|
{a,b,c} means the set consisting of a, b, and c.[7] | ℕ = { 1, 2, 3, ... } |
{ : } { | } { ; } |
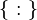 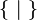 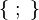 |
set builder notation
the set of ... such that
|
{x : P(x)} means the set of all x for which P(x) is true.[7] {x | P(x)} is the same as {x : P(x)}. | {n ∈ ℕ : n2 < 20} = { 1, 2, 3, 4 } |
⌊...⌋ |
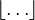 |
floor;
greatest integer; entier |
⌊x⌋ means the floor of x, i.e. the largest integer less than or equal to x. (This may also be written [x], floor(x) or int(x).) |
⌊4⌋ = 4, ⌊2.1⌋ = 2, ⌊2.9⌋ = 2, ⌊−2.6⌋ = −3 |
⌈...⌉ |
 |
ceiling
|
⌈x⌉ means the ceiling of x, i.e. the smallest integer greater than or equal to x. (This may also be written ceil(x) or ceiling(x).) |
⌈4⌉ = 4, ⌈2.1⌉ = 3, ⌈2.9⌉ = 3, ⌈−2.6⌉ = −2 |
⌊...⌉ |
 |
nearest integer to
|
⌊x⌉ means the nearest integer to x. (This may also be written [x], ||x||, nint(x) or Round(x).) |
⌊2⌉ = 2, ⌊2.6⌉ = 3, ⌊-3.4⌉ = -3, ⌊4.49⌉ = 4 |
[ : ] |
![[\ :\ ] \!\,](../I/m/39d5340377c7738ba4f72a9739f63afe.png) |
the degree of
field theory |
[K : F] means the degree of the extension K : F. | [ℚ(√2) : ℚ] = 2 [ℂ : ℝ] = 2 [ℝ : ℚ] = ∞ |
![[\ ] \!\,](../I/m/c2dc57d3486acdb1ec8efad3719a2757.png) ![[\ ,\ ] \!\,](../I/m/691075e7366c90a8857edd45a2053aa8.png) ![[\ ,\ ,\ ] \!\,](../I/m/f2a7f66d6e7f58cba58ee0148f6b824e.png) |
the equivalence class of
|
[a] means the equivalence class of a, i.e. {x : x ~ a}, where ~ is an equivalence relation. [a]R means the same, but with R as the equivalence relation. |
Let a ~ b be true iff a ≡ b (mod 5).
Then [2] = {..., −8, −3, 2, 7, ...}. | |
|
floor;
greatest integer; entier |
[x] means the floor of x, i.e. the largest integer less than or equal to x. (This may also be written ⌊x⌋, floor(x) or int(x). Not to be confused with the nearest integer function, as described below.) |
[3] = 3, [3.5] = 3, [3.99] = 3, [−3.7] = −4 | ||
|
nearest integer to
|
[x] means the nearest integer to x. (This may also be written ⌊x⌉, ||x||, nint(x) or Round(x). Not to be confused with the floor function, as described above.) |
[2] = 2, [2.6] = 3, [-3.4] = -3, [4.49] = 4 | ||
|
1 if true, 0 otherwise
propositional logic |
[S] maps a true statement S to 1 and a false statement S to 0. | [0=5]=0, [7>0]=1, [2 ∈ {2,3,4}]=1, [5 ∈ {2,3,4}]=0 | ||
|
image of ... under ...
everywhere |
f[X] means { f(x) : x ∈ X }, the image of the function f under the set X ⊆ dom(f). (This may also be written as f(X) if there is no risk of confusing the image of f under X with the function application f of X. Another notation is Im f, the image of f under its domain.) |
![\sin [\mathbb{R}] = [-1, 1]](../I/m/a0d9d93cb1bf77d49afcd6590af9f78e.png) | ||
|
closed interval
closed interval
|
![[a,b] = \{x \in \mathbb{R} : a \le x \le b \}](../I/m/d6fb4b1478e9c68e216dcf78d4941dca.png) . . |
0 and 1/2 are in the interval [0,1]. | ||
|
the commutator of
|
[g, h] = g−1h−1gh (or ghg−1h−1), if g, h ∈ G (a group). [a, b] = ab − ba, if a, b ∈ R (a ring or commutative algebra). |
xy = x[x, y] (group theory). [AB, C] = A[B, C] + [A, C]B (ring theory). | ||
|
triple scalar product
the triple scalar product of
|
[a, b, c] = a × b · c, the scalar product of a × b with c. | [a, b, c] = [b, c, a] = [c, a, b]. | ||
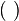  |
function application
of
|
f(x) means the value of the function f at the element x. | If f(x) := x2, then f(3) = 32 = 9. | |
|
image of ... under ...
everywhere |
f(X) means { f(x) : x ∈ X }, the image of the function f under the set X ⊆ dom(f). (This may also be written as f[X] if there is a risk of confusing the image of f under X with the function application f of X. Another notation is Im f, the image of f under its domain.) |
![\sin (\mathbb{R}) = [-1, 1]](../I/m/f3a08fa415b1ea34de05851776980a28.png) | ||
|
precedence grouping
parentheses
everywhere |
Perform the operations inside the parentheses first. | (8/4)/2 = 2/2 = 1, but 8/(4/2) = 8/2 = 4. | ||
|
tuple; n-tuple;
ordered pair/triple/etc; row vector; sequence everywhere |
An ordered list (or sequence, or horizontal vector, or row vector) of values.
(Note that the notation (a,b) is ambiguous: it could be an ordered pair or an open interval. Set theorists and computer scientists often use angle brackets ⟨ ⟩ instead of parentheses.) |
(a, b) is an ordered pair (or 2-tuple).
(a, b, c) is an ordered triple (or 3-tuple). ( ) is the empty tuple (or 0-tuple). | ||
|
highest common factor
highest common factor;
greatest common divisor; hcf; gcd number theory |
(a, b) means the highest common factor of a and b. (This may also be written hcf(a, b) or gcd(a, b).) |
(3, 7) = 1 (they are coprime); (15, 25) = 5. | ||
( , ) ] , [ |
 ![]\ ,\ [ \!\,](../I/m/56ae0d842e03b2b7504f316f176a3467.png) |
open interval
open interval
|
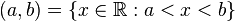 . .
(Note that the notation (a,b) is ambiguous: it could be an ordered pair or an open interval. The notation ]a,b[ can be used instead.) |
4 is not in the interval (4, 18).
(0, +∞) equals the set of positive real numbers. |
( , ] ] , ] |
![(\ ,\ ] \!\,](../I/m/b2217c84cbe375b0506b8429a6f69258.png) ![]\ ,\ ] \!\,](../I/m/1f129e23b31f26cf551000acaed7e18c.png) |
left-open interval
half-open interval;
left-open interval |
![(a,b] = \{x \in \mathbb{R} : a < x \le b \}](../I/m/da9d325123d50dbc4e36363f2863ce3e.png) . . |
(−1, 7] and (−∞, −1] |
[ , ) [ , [ |
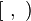  |
right-open interval
half-open interval;
right-open interval |
 . . |
[4, 18) and [1, +∞) |
⟨⟩ ⟨,⟩ |
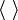  |
inner product
inner product of
|
⟨u,v⟩ means the inner product of u and v, where u and v are members of an inner product space. Note that the notation ⟨u, v⟩ may be ambiguous: it could mean the inner product or the linear span. There are many variants of the notation, such as ⟨u | v⟩ and (u | v), which are described below. For spatial vectors, the dot product notation, x · y is common. For matrices, the colon notation A : B may be used. As ⟨ and ⟩ can be hard to type, the more "keyboard friendly" forms < and > are sometimes seen. These are avoided in mathematical texts. |
The standard inner product between two vectors x = (2, 3) and y = (−1, 5) is: ⟨x, y⟩ = 2 × −1 + 3 × 5 = 13 |
|
average
average of
|
let S be a subset of N for example, 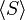 represents the average of all the element in S. represents the average of all the element in S. |
for a time series :g(t) (t = 1, 2,...)
we can define the structure functions Sq( | ||
|
(linear) span of;
linear hull of |
⟨S⟩ means the span of S ⊆ V. That is, it is the intersection of all subspaces of V which contain S. ⟨u1, u2, ...⟩ is shorthand for ⟨{u1, u2, ...}⟩.
|
 . . | ||
|
subgroup generated by a set
the subgroup generated by
|
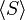 means the smallest subgroup of G (where S ⊆ G, a group) containing every element of S. means the smallest subgroup of G (where S ⊆ G, a group) containing every element of S. is shorthand for is shorthand for 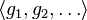 . . |
In S3, 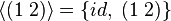 and and  . . | ||
|
tuple; n-tuple;
ordered pair/triple/etc; row vector; sequence everywhere |
An ordered list (or sequence, or horizontal vector, or row vector) of values.
(The notation (a,b) is often used as well.) |
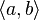 is an ordered pair (or 2-tuple). is an ordered pair (or 2-tuple).
| ||
⟨|⟩ (|) |
 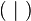 |
inner product
inner product of
|
⟨u | v⟩ means the inner product of u and v, where u and v are members of an inner product space.[8] (u | v) means the same. Another variant of the notation is ⟨u, v⟩ which is described above. For spatial vectors, the dot product notation, x · y is common. For matrices, the colon notation A : B may be used. As ⟨ and ⟩ can be hard to type, the more "keyboard friendly" forms < and > are sometimes seen. These are avoided in mathematical texts. |
Other non-letter symbols
| Symbol in HTML |
Symbol in TeX |
Name | Explanation | Examples |
|---|---|---|---|---|
| Read as | ||||
| Category | ||||
 |
convolution;
convolved with |
f ∗ g means the convolution of f and g. | 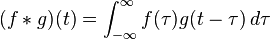 . . | |
|
conjugate
complex numbers |
z∗ means the complex conjugate of z. ( 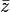 can also be used for the conjugate of z, as described below.) can also be used for the conjugate of z, as described below.) |
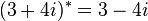 . . | ||
|
group of units
the group of units of
|
R∗ consists of the set of units of the ring R, along with the operation of multiplication. This may also be written R× as described above, or U(R). |
![\begin{align} (\mathbb{Z} / 5\mathbb{Z})^\ast & = \{ [1], [2], [3], [4] \} \\ & \cong \mathrm{C}_4 \\ \end{align}](../I/m/445445fdaf4d7fa564c90e04d05f0162.png) | ||
|
the (set of) hyperreals
|
∗R means the set of hyperreal numbers. Other sets can be used in place of R. | ∗N is the hypernatural numbers. | ||
|
Hodge dual;
Hodge star |
∗v means the Hodge dual of a vector v. If v is a k-vector within an n-dimensional oriented inner product space, then ∗v is an (n−k)-vector. | If 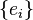 are the standard basis vectors of are the standard basis vectors of 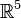 , ,  | ||
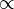 |
is proportional to;
varies as everywhere |
y ∝ x means that y = kx for some constant k. | if y = 2x, then y ∝ x. | |
|
Karp reduction[9]
is Karp reducible to;
is polynomial-time many-one reducible to |
A ∝ B means the problem A can be polynomially reduced to the problem B. | If L1 ∝ L2 and L2 ∈ P, then L1 ∈ P. | ||
∖ |
 |
minus;
without |
A ∖ B means the set that contains all those elements of A that are not in B.[5] (− can also be used for set-theoretic complement as described above.) |
{1,2,3,4} ∖ {3,4,5,6} = {1,2} |
 |
given
|
P(A|B) means the probability of the event A occurring given that B occurs. | if X is a uniformly random day of the year P(X is May 25 | X is in May) = 1/31 | |
|
restriction of ... to ...;
restricted to |
f|A means the function f is restricted to the set A, that is, it is the function with domain A ∩ dom(f) that agrees with f. | The function f : R → R defined by f(x) = x2 is not injective, but f|R+ is injective. | ||
|
such that
such that;
so that everywhere |
| means "such that", see ":" (described below). | S = {(x,y) | 0 < y < f(x)} The set of (x,y) such that y is greater than 0 and less than f(x). | ||
∣ ∤ |
 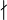 |
divides
|
a ∣ b means a divides b. a ∤ b means a does not divide b. (The symbol ∣ can be difficult to type, and its negation is rare, so a regular but slightly shorter vertical bar | character is often used instead.) |
Since 15 = 3 × 5, it is true that 3 ∣ 15 and 5 ∣ 15. |
∣∣ |
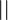 |
exact divisibility
exactly divides
|
pa ∣∣ n means pa exactly divides n (i.e. pa divides n but pa+1 does not). | 23 ∣∣ 360. |
∥ ∦ ⋕ |
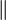 |
is parallel to
|
x ∥ y means x is parallel to y. x ∦ y means x is not parallel to y. x ⋕ y means x is equal and parallel to y. (The symbol ∥ can be difficult to type, and its negation is rare, so two regular but slightly longer vertical bar || characters are often used instead.) |
If l ∥ m and m ⊥ n then l ⊥ n. |
|
is incomparable to
|
x ∥ y means x is incomparable to y. | {1,2} ∥ {2,3} under set containment. | ||
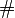 |
cardinality of;
size of; order of |
#X means the cardinality of the set X. (|...| may be used instead as described above.) |
#{4, 6, 8} = 3 | |
|
connected sum of;
knot sum of; knot composition of |
A#B is the connected sum of the manifolds A and B. If A and B are knots, then this denotes the knot sum, which has a slightly stronger condition. | A#Sm is homeomorphic to A, for any manifold A, and the sphere Sm. | ||
|
primorial
|
n# is product of all prime numbers less than or equal to n. | 12# = 2 × 3 × 5 × 7 × 11 = 2310 | ||
 |
such that
such that;
so that everywhere |
: means "such that", and is used in proofs and the set-builder notation (described below). | ∃ n ∈ ℕ: n is even. | |
|
extends;
over field theory |
K : F means the field K extends the field F. This may also be written as K ≥ F. |
ℝ : ℚ | ||
|
inner product of matrices
inner product of
|
A : B means the Frobenius inner product of the matrices A and B. The general inner product is denoted by ⟨u, v⟩, ⟨u | v⟩ or (u | v), as described below. For spatial vectors, the dot product notation, x·y is common. See also bra–ket notation. |
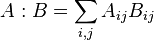 | ||
|
index of subgroup
|
The index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" (cosets) of H that fill up G |  | ||
|
divided by
over everywhere |
A : B means the division of A with B (dividing A by B) | 10 : 2 = 5 | ||
⋮ |
 |
vertical ellipsis
vertical ellipsis
everywhere |
Denotes that certain constants and terms are missing out (e.g. for clarity) and that only the important terms are being listed. |  |
≀ |
 |
wreath product of ... by ...
|
A ≀ H means the wreath product of the group A by the group H. This may also be written A wr H. |
 is isomorphic to the automorphism group of the complete bipartite graph on (n,n) vertices. is isomorphic to the automorphism group of the complete bipartite graph on (n,n) vertices. |
↯ |
contradiction; this contradicts that
everywhere |
Denotes that contradictory statements have been inferred. For clarity, the exact point of contradiction can be appended. | Statement: Every finite, non-empty, ordered set has a largest element. Otherwise, let's assume that  is a finite, non-empty, ordered set with no largest element. Then, for some is a finite, non-empty, ordered set with no largest element. Then, for some 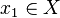 , there exists an , there exists an  with with 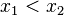 , but then there's also an , but then there's also an  with with 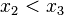 , and so on. Thus, , and so on. Thus, 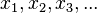 are distinct elements in are distinct elements in  . ↯ . ↯  is finite. is finite. | |
⊕ ⊻ |
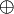 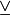 |
xor
propositional logic, Boolean algebra |
The statement A ⊕ B is true when either A or B, but not both, are true. A ⊻ B means the same. | (¬A) ⊕ A is always true, A ⊕ A is always false. |
|
direct sum of
|
The direct sum is a special way of combining several objects into one general object. (The bun symbol ⊕, or the coproduct symbol ∐, is used; ⊻ is only for logic.) |
Most commonly, for vector spaces U, V, and W, the following consequence is used: U = V ⊕ W ⇔ (U = V + W) ∧ (V ∩ W = {0}) | ||
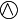 |
Kulkarni–Nomizu product
|
Derived from the tensor product of two symmetric type (0,2) tensors; it has the algebraic symmetries of the Riemann tensor.  has components has components  . . |
||
□ |
 |
D'Alembertian
non-Euclidean Laplacian
|
It is the generalisation of the Laplace operator in the sense that it is the differential operator which is invariant under the isometry group of the underlying space and it reduces to the Laplace operator if restricted to time independent functions. |  |
Letter-based symbols
Includes upside-down letters.
Letter modifiers
| Symbol in HTML |
Symbol in TeX |
Name | Explanation | Examples |
|---|---|---|---|---|
| Read as | ||||
| Category | ||||
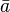 |
overbar;
... bar |
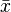 (often read as "x bar") is the mean (average value of (often read as "x bar") is the mean (average value of 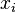 ). ). |
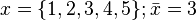 . . | |
|
finite sequence, tuple
|
 means the finite sequence/tuple means the finite sequence/tuple  . . |
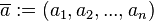 . . | ||
|
algebraic closure of
field theory |
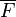 is the algebraic closure of the field F. is the algebraic closure of the field F. |
The field of algebraic numbers is sometimes denoted as 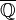 because it is the algebraic closure of the rational numbers because it is the algebraic closure of the rational numbers  . . | ||
|
conjugate
complex numbers |
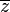 means the complex conjugate of z. means the complex conjugate of z.(z∗ can also be used for the conjugate of z, as described above.) |
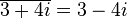 . . | ||
|
topological closure
(topological) closure of
|
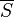 is the topological closure of the set S. is the topological closure of the set S.This may also be denoted as cl(S) or Cl(S). |
In the space of the real numbers, 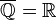 (the rational numbers are dense in the real numbers). (the rational numbers are dense in the real numbers). | ||
â |
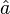 |
hat
|
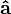 (pronounced "a hat") is the normalized version of vector (pronounced "a hat") is the normalized version of vector 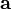 , having length 1. , having length 1. |
|
|
estimator for
|
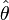 is the estimator or the estimate for the parameter is the estimator or the estimate for the parameter  . . |
The estimator  produces a sample estimate produces a sample estimate 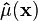 for the mean for the mean  . . | ||
 |
... prime;
derivative of |
f ′(x) means the derivative of the function f at the point x, i.e., the slope of the tangent to f at x. (The single-quote character ' is sometimes used instead, especially in ASCII text.) |
If f(x) := x2, then f ′(x) = 2x. | |
• |
 |
... dot;
time derivative of |
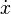 means the derivative of x with respect to time. That is means the derivative of x with respect to time. That is 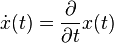 . . |
If x(t) := t2, then 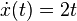 . . |
Symbols based on Latin letters
| Symbol in HTML |
Symbol in TeX |
Name | Explanation | Examples |
|---|---|---|---|---|
| Read as | ||||
| Category
| ||||
∀ |
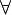 |
for all;
for any; for each |
∀ x: P(x) means P(x) is true for all x. | ∀ n ∈ ℕ: n2 ≥ n. |
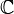 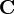 |
C;
the (set of) complex numbers |
ℂ means {a + b i : a,b ∈ ℝ}. | i = √(−1) ∈ ℂ | |
𝔠 |
 |
cardinality of the continuum;
c; cardinality of the real numbers |
The cardinality of 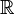 is denoted by is denoted by 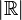 or by the symbol or by the symbol  (a lowercase Fraktur letter C). (a lowercase Fraktur letter C). |
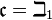
|
∂ |
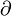 |
partial;
d |
∂f/∂xi means the partial derivative of f with respect to xi, where f is a function on (x1, ..., xn). | If f(x,y) := x2y, then ∂f/∂x = 2xy, |
|
boundary of
|
∂M means the boundary of M | ∂{x : ||x|| ≤ 2} = {x : ||x|| = 2} | ||
|
degree of
|
∂f means the degree of the polynomial f. (This may also be written deg f.) |
∂(x2 − 1) = 2 | ||
𝔼 E |
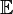 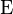 |
expected value
|
the value of a random variable one would "expect" to find if one could repeat the random variable process an infinite number of times and take the average of the values obtained | ![\mathbb{E}[X] = \frac{x_1p_1 + x_2p_2 + \dotsb + x_kp_k}{p_1 + p_2 + \dotsb + p_k}](../I/m/39995abe95296dc0228885bee374ed91.png) |
∃ |
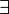 |
there exists;
there is; there are |
∃ x: P(x) means there is at least one x such that P(x) is true. | ∃ n ∈ ℕ: n is even. |
∃! |
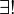 |
there exists exactly one
|
∃! x: P(x) means there is exactly one x such that P(x) is true. | ∃! n ∈ ℕ: n + 5 = 2n. |
∈ ∉ |
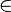 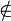 |
is an element of;
is not an element of everywhere, set theory |
a ∈ S means a is an element of the set S;[7] a ∉ S means a is not an element of S.[7] | (1/2)−1 ∈ ℕ 2−1 ∉ ℕ |
∌ |
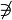 |
does not contain as an element
|
S ∌ e means the same thing as e ∉ S, where S is a set and e is not an element of S. | |
∋ |
 |
such that symbol
such that
|
often abbreviated as "s.t."; : and | are also used to abbreviate "such that". The use of ∋ goes back to early mathematical logic and its usage in this sense is declining. | Choose  ∋ 2| ∋ 2| and 3| and 3| . (Here | is used in the sense of "divides".) . (Here | is used in the sense of "divides".) |
|
contains as an element
|
S ∋ e means the same thing as e ∈ S, where S is a set and e is an element of S. | |||
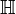 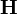 |
quaternions or Hamiltonian quaternions
H;
the (set of) quaternions |
ℍ means {a + b i + c j + d k : a,b,c,d ∈ ℝ}. | ||
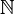 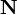 |
the (set of) natural numbers
|
N means either { 0, 1, 2, 3, ...} or { 1, 2, 3, ...}. The choice depends on the area of mathematics being studied; e.g. number theorists prefer the latter; analysts, set theorists and computer scientists prefer the former. To avoid confusion, always check an author's definition of N. Set theorists often use the notation ω (for least infinite ordinal) to denote the set of natural numbers (including zero), along with the standard ordering relation ≤. |
ℕ = {|a| : a ∈ ℤ} or ℕ = {|a| > 0: a ∈ ℤ} | |
o |
 |
entrywise product
|
For two matrices (or vectors) of the same dimensions 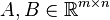 the Hadamard product is a matrix of the same dimensions the Hadamard product is a matrix of the same dimensions 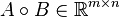 with elements given by with elements given by 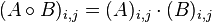 . .In MATLAB this operation is expressed by A.*B.) |
 |
∘ |
 |
composed with
|
f ∘ g is the function such that (f ∘ g)(x) = f(g(x)).[10] | if f(x) := 2x, and g(x) := x + 3, then (f ∘ g)(x) = 2(x + 3). |
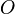 |
big-oh of
|
The Big O notation describes the limiting behavior of a function, when the argument tends towards a particular value or infinity. | If f(x) = 6x4 − 2x3 + 5 and g(x) = x4, then 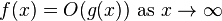
| |
 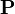 |
P;
the projective space; the projective line; the projective plane |
ℙ means a space with a point at infinity. | 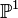 , ,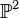 | |
|
the probability of
|
ℙ(X) means the probability of the event X occurring. This may also be written as P(X), Pr(X), P[X] or Pr[X]. |
If a fair coin is flipped, ℙ(Heads) = ℙ(Tails) = 0.5. | ||
|
the Power set of
Powerset |
Given a set S, the power set of S is the set of all subsets of the set S. The power set of S0 is
denoted by P(S). |
The power set P({0, 1, 2}) is the set of all subsets of {0, 1, 2}. Hence,
P({0, 1, 2}) = {∅, {0}, {1}, {2}, {0, 1}, {0, 2}, {1, 2}, {0, 1, 2. }} | ||
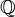 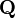 |
Q;
the (set of) rational numbers; the rationals |
ℚ means {p/q : p ∈ ℤ, q ∈ ℕ}. | 3.14000... ∈ ℚ π ∉ ℚ | |
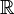  |
R;
the (set of) real numbers; the reals |
ℝ means the set of real numbers. | π ∈ ℝ √(−1) ∉ ℝ | |
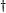 |
conjugate transpose;
adjoint; Hermitian adjoint/conjugate/transpose matrix operations |
A† means the transpose of the complex conjugate of A.[11] This may also be written A∗T, AT∗, A∗, AT or AT. |
If A = (aij) then A† = (aji). | |
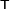 |
transpose
matrix operations |
AT means A, but with its rows swapped for columns. This may also be written A′, At or Atr. |
If A = (aij) then AT = (aji). | |
 |
the top element
|
⊤ means the largest element of a lattice. | ∀x : x ∨ ⊤ = ⊤ | |
|
the top type; top
|
⊤ means the top or universal type; every type in the type system of interest is a subtype of top. | ∀ types T, T <: ⊤ | ||
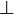 |
is perpendicular to
|
x ⊥ y means x is perpendicular to y; or more generally x is orthogonal to y. | If l ⊥ m and m ⊥ n in the plane, then l || n. | |
|
orthogonal/ perpendicular complement of;
perp |
W⊥ means the orthogonal complement of W (where W is a subspace of the inner product space V), the set of all vectors in V orthogonal to every vector in W. | Within 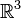 , , 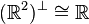 . . | ||
|
coprime
is coprime to
|
x ⊥ y means x has no factor greater than 1 in common with y. | 34 ⊥ 55 | ||
|
is independent of
|
A ⊥ B means A is an event whose probability is independent of event B. | If A ⊥ B, then P(A|B) = P(A). | ||
|
bottom element
the bottom element
|
⊥ means the smallest element of a lattice. | ∀x : x ∧ ⊥ = ⊥ | ||
|
the bottom type;
bot |
⊥ means the bottom type (a.k.a. the zero type or empty type); bottom is the subtype of every type in the type system. | ∀ types T, ⊥ <: T | ||
|
is comparable to
|
x ⊥ y means that x is comparable to y. | {e, π} ⊥ {1, 2, e, 3, π} under set containment. | ||
∪ |
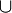 |
the union of ... or ...;
union |
A ∪ B means the set of those elements which are either in A, or in B, or in both.[5] | A ⊆ B ⇔ (A ∪ B) = B |
∩ |
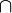 |
intersected with;
intersect |
A ∩ B means the set that contains all those elements that A and B have in common.[5] | {x ∈ ℝ : x2 = 1} ∩ ℕ = {1} |
∨ |
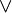 |
logical disjunction or join in a lattice
or;
max; join propositional logic, lattice theory |
The statement A ∨ B is true if A or B (or both) are true; if both are false, the statement is false. For functions A(x) and B(x), A(x) ∨ B(x) is used to mean max(A(x), B(x)). |
n ≥ 4 ∨ n ≤ 2 ⇔ n ≠ 3 when n is a natural number. |
∧ |
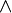 |
logical conjunction or meet in a lattice
propositional logic, lattice theory |
The statement A ∧ B is true if A and B are both true; else it is false. For functions A(x) and B(x), A(x) ∧ B(x) is used to mean min(A(x), B(x)). |
n < 4 ∧ n > 2 ⇔ n = 3 when n is a natural number. |
|
wedge product
wedge product;
exterior product |
u ∧ v means the wedge product of any multivectors u and v. In three-dimensional Euclidean space the wedge product and the cross product of two vectors are each other's Hodge dual. | 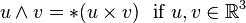 | ||
|
... (raised) to the power of ...
everywhere |
a ^ b means a raised to the power of b (a ^ b is more commonly written ab. The symbol ^ is generally used in programming languages where ease of typing and use of plain ASCII text is preferred.) |
2^3 = 23 = 8 | ||
 |
times;
multiplied by |
3 × 4 means the multiplication of 3 by 4. (The symbol * is generally used in programming languages, where ease of typing and use of ASCII text is preferred.) |
7 × 8 = 56 | |
|
the Cartesian product of ... and ...;
the direct product of ... and ... |
X × Y means the set of all ordered pairs with the first element of each pair selected from X and the second element selected from Y. | {1,2} × {3,4} = {(1,3),(1,4),(2,3),(2,4)} | ||
|
cross
|
u × v means the cross product of vectors u and v | (1,2,5) × (3,4,−1) = (−22, 16, − 2) | ||
|
group of units
the group of units of
|
R× consists of the set of units of the ring R, along with the operation of multiplication. This may also be written R∗ as described below, or U(R). |
![\begin{align} (\mathbb{Z} / 5\mathbb{Z})^\times & = \{ [1], [2], [3], [4] \} \\ & \cong \mathrm{C}_4 \\ \end{align}](../I/m/9b2a5650da1bc96e6299694c6a967636.png) | ||
⊗ |
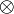 |
tensor product of
|
 means the tensor product of V and U.[12] means the tensor product of V and U.[12] 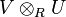 means the tensor product of modules V and U over the ring R. means the tensor product of modules V and U over the ring R. |
{1, 2, 3, 4} ⊗ {1, 1, 2} = {{1, 1, 2}, {2, 2, 4}, {3, 3, 6}, {4, 4, 8}} |
⋉ ⋊ |
 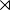 |
the semidirect product of
|
N ⋊φ H is the semidirect product of N (a normal subgroup) and H (a subgroup), with respect to φ. Also, if G = N ⋊φ H, then G is said to split over N. (⋊ may also be written the other way round, as ⋉, or as ×.) |
 |
|
semijoin
the semijoin of
|
R ⋉ S is the semijoin of the relations R and S, the set of all tuples in R for which there is a tuple in S that is equal on their common attribute names. | R  S = S = 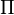 a1,..,an(R a1,..,an(R 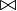 S) S) | ||
⋈ |
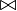 |
natural join
the natural join of
|
R ⋈ S is the natural join of the relations R and S, the set of all combinations of tuples in R and S that are equal on their common attribute names. |
|
 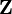 |
the (set of) integers
|
ℤ means {..., −3, −2, −1, 0, 1, 2, 3, ...}.
ℤ+ or ℤ> means {1, 2, 3, ...} . |
ℤ = {p, −p : p ∈ ℕ ∪ {0}} | |
ℤn ℤp Zn Zp |
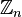 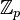 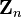 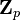 |
the (set of) integers modulo n
|
ℤn means {[0], [1], [2], ...[n−1]} with addition and multiplication modulo n. Note that any letter may be used instead of n, such as p. To avoid confusion with p-adic numbers, use ℤ/pℤ or ℤ/(p) instead. |
ℤ3 = {[0], [1], [2]} |
|
p-adic integers
the (set of) p-adic integers
|
Note that any letter may be used instead of p, such as n or l. |
Symbols based on Hebrew or Greek letters
| Symbol in HTML |
Symbol in TeX |
Name | Explanation | Examples |
|---|---|---|---|---|
| Read as | ||||
| Category | ||||
ℵ |
 |
aleph
|
ℵα represents an infinite cardinality (specifically, the α-th one, where α is an ordinal). | |ℕ| = ℵ0, which is called aleph-null. |
ℶ |
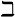 |
beth
|
ℶα represents an infinite cardinality (similar to ℵ, but ℶ does not necessarily index all of the numbers indexed by ℵ. ). | 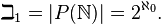 |
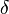 |
Dirac delta of
|
 |
δ(x) | |
|
Kronecker delta of
|
 |
δij | ||
|
Functional derivative of
Differential operators |
![\begin{align}
\left\langle \frac{\delta F[\varphi(x)]}{\delta\varphi(x)}, f(x) \right\rangle
&= \int \frac{\delta F[\varphi(x)]}{\delta\varphi(x')} f(x')dx' \\
&= \lim_{\varepsilon\to 0}\frac{F[\varphi(x)+\varepsilon f(x)]-F[\varphi(x)]}{\varepsilon} \\
&= \left.\frac{d}{d\epsilon}F[\varphi+\epsilon f]\right|_{\epsilon=0}.
\end{align}](../I/m/917a8fdafeb796b09a884ed975eba966.png) |
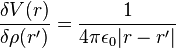 | ||
∆ ⊖ |
 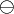 |
symmetric difference
|
A ∆ B (or A ⊖ B) means the set of elements in exactly one of A or B. (Not to be confused with delta, Δ, described below.) |
{1,5,6,8} ∆ {2,5,8} = {1,2,6} {3,4,5,6} ⊖ {1,2,5,6} = {1,2,3,4} |
 |
delta;
change in |
Δx means a (non-infinitesimal) change in x. (If the change becomes infinitesimal, δ and even d are used instead. Not to be confused with the symmetric difference, written ∆, above.) |
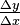 is the gradient of a straight line. is the gradient of a straight line. | |
|
Laplacian
Laplace operator
|
The Laplace operator is a second order differential operator in n-dimensional Euclidean space | If ƒ is a twice-differentiable real-valued function, then the Laplacian of ƒ is defined by 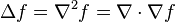 | ||
 |
∇f (x1, ..., xn) is the vector of partial derivatives (∂f / ∂x1, ..., ∂f / ∂xn). | If f (x,y,z) := 3xy + z², then ∇f = (3y, 3x, 2z) | ||
|
del dot;
divergence of |
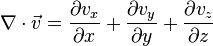 |
If  , then , then 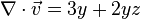 . . | ||
|
curl of
|
  |
If  , then , then 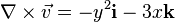 . . | ||
 |
pi;
3.1415926...; ≈22÷7 |
Used in various formulas involving circles; π is equivalent to the amount of area a circle would take up in a square of equal width with an area of 4 square units, roughly 3.14159. It is also the ratio of the circumference to the diameter of a circle. | A = πR2 = 314.16 → R = 10 | |
|
Projection of
|
 restricts restricts  to the to the 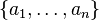 attribute set. attribute set. |
 | ||
|
the nth Homotopy group of
Homotopy theory |
 consists of homotopy equivalence classes of base point preserving maps from an n-dimensional sphere (with base point) into the pointed space X. consists of homotopy equivalence classes of base point preserving maps from an n-dimensional sphere (with base point) into the pointed space X. |
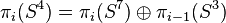 | ||
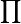 |
product over ... from ... to ... of
|
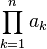 means means 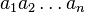 . . |
 | |
|
the Cartesian product of;
the direct product of |
 means the set of all (n+1)-tuples means the set of all (n+1)-tuples
|
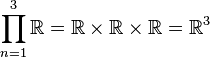 | ||
∐ |
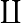 |
coproduct over ... from ... to ... of
|
A general construction which subsumes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the "least specific" object to which each object in the family admits a morphism. | |
 |
Selection of
|
The selection  selects all those tuples in selects all those tuples in  for which for which  holds between the holds between the  and the and the  attribute. The selection attribute. The selection 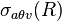 selects all those tuples in selects all those tuples in  for which for which  holds between the holds between the  attribute and the value attribute and the value  . . |
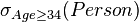 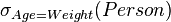 | |
∑ |
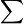 |
sum over ... from ... to ... of
|
 means means  . . |
 |
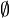 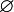  |
the empty set
|
∅ means the set with no elements.[7] { } means the same. | {n ∈ ℕ : 1 < n2 < 4} = ∅ |
Variations
In mathematics written in Arabic, some symbols may be reversed to make right-to-left writing and reading easier.[13]
See also
- Greek letters used in mathematics, science, and engineering
- ISO 31-11 (Mathematical signs and symbols for use in physical sciences and technology)
- Latin letters used in mathematics
- List of mathematical abbreviations
- List of mathematical symbols by subject
- Mathematical alphanumeric symbols
- Mathematical constants and functions
- Mathematical notation
- Mathematical operators and symbols in Unicode
- Notation in probability and statistics
- Physical constants
- Table of logic symbols
- Table of mathematical symbols by introduction date
- Typographical conventions in mathematical formulae
References
- ↑ "Math is Fun website".
- ↑ Rónyai, Lajos (1998), Algoritmusok(Algorithms), TYPOTEX, ISBN 963-9132-16-0
- ↑ Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. (2002). "A fast and elitist multiobjective genetic algorithm: NSGA-II". IEEE Transactions on Evolutionary Computation 6 (2): 182. doi:10.1109/4235.996017.
- ↑ Copi, Irving M.; Cohen, Carl (1990) [1953], "Chapter 8.3: Conditional Statements and Material Implication", Introduction to Logic (8th ed.), New York: Macmillan Publishers (United States), pp. 268–269, ISBN 0-02-325035-6, LCCN 89037742
- ↑ 5.0 5.1 5.2 5.3 Goldrei, Derek (1996), Classic Set Theory, London: Chapman and Hall, p. 4, ISBN 0-412-60610-0
- ↑ Nielsen, Michael A; Chuang, Isaac L (2000), Quantum Computation and Quantum Information, New York: Cambridge University Press, p. 66, ISBN 0-521-63503-9, OCLC 43641333
- ↑ 7.0 7.1 7.2 7.3 7.4 Goldrei, Derek (1996), Classic Set Theory, London: Chapman and Hall, p. 3, ISBN 0-412-60610-0
- ↑ Nielsen, Michael A; Chuang, Isaac L (2000), Quantum Computation and Quantum Information, New York: Cambridge University Press, p. 62, ISBN 0-521-63503-9, OCLC 43641333
- ↑ Berman, Kenneth A; Paul, Jerome L. (2005), Algorithms: Sequential, Parallel, and Distributed, Boston: Course Technology, p. 822, ISBN 0-534-42057-5
- ↑ Goldrei, Derek (1996), Classic Set Theory, London: Chapman and Hall, p. 5, ISBN 0-412-60610-0
- ↑ Nielsen, Michael A; Chuang, Isaac L (2000), Quantum Computation and Quantum Information, New York: Cambridge University Press, pp. 69–70, ISBN 0-521-63503-9, OCLC 43641333
- ↑ Nielsen, Michael A; Chuang, Isaac L (2000), Quantum Computation and Quantum Information, New York: Cambridge University Press, pp. 71–72, ISBN 0-521-63503-9, OCLC 43641333
- ↑ M. Benatia, A. Lazrik, and K. Sami, "Arabic mathematical symbols in Unicode", 27th Internationalization and Unicode Conference, 2005.
External links
- The complete set of mathematics Unicode characters
- Jeff Miller: Earliest Uses of Various Mathematical Symbols
- Numericana: Scientific Symbols and Icons
- GIF and PNG Images for Math Symbols
- Mathematical Symbols in Unicode
- Using Greek and special characters from Symbol font in HTML
- Unicode Math Symbols - a quick form for using unicode math symbols.
- DeTeXify handwritten symbol recognition — doodle a symbol in the box, and the program will tell you what its name is
Some Unicode charts of mathematical operators:
- Index of Unicode symbols
- Range 2100–214F: Unicode Letterlike Symbols
- Range 2190–21FF: Unicode Arrows
- Range 2200–22FF: Unicode Mathematical Operators
- Range 27C0–27EF: Unicode Miscellaneous Mathematical Symbols–A
- Range 2980–29FF: Unicode Miscellaneous Mathematical Symbols–B
- Range 2A00–2AFF: Unicode Supplementary Mathematical Operators
Some Unicode cross-references:
- Short list of commonly used LaTeX symbols and Comprehensive LaTeX Symbol List
- MathML Characters - sorts out Unicode, HTML and MathML/TeX names on one page
- Unicode values and MathML names
- Unicode values and Postscript names from the source code for Ghostscript
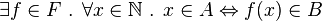


 ):
):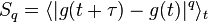
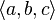 is an ordered triple (or 3-tuple).
is an ordered triple (or 3-tuple). is the empty tuple (or 0-tuple).
is the empty tuple (or 0-tuple).