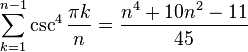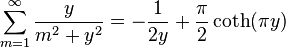List of mathematical series
This list of mathematical series contains formulae for finite and infinite sums. It can be used in conjunction with other tools for evaluating sums.
- Here,
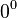 is taken to have the value 1.
is taken to have the value 1. 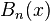 is a Bernoulli polynomial.
is a Bernoulli polynomial.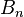 is a Bernoulli number, and here,
is a Bernoulli number, and here, 
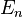 is an Euler number.
is an Euler number.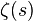 is the Riemann zeta function.
is the Riemann zeta function.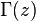 is the gamma function.
is the gamma function.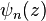 is a polygamma function.
is a polygamma function.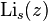 is a polylogarithm.
is a polylogarithm.
Sums of powers
See Faulhaber's formula.
The first few values are:
See zeta constants.
The first few values are:
 (the Basel problem)
(the Basel problem)
Power series
Low-order polylogarithms
Finite sums:
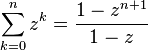 , (geometric series)
, (geometric series)
Infinite sums, valid for 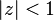 (see polylogarithm):
(see polylogarithm):
The following is a useful property to calculate low-integer-order polylogarithms recursively in closed form:
Exponential function
 (cf. mean of Poisson distribution)
(cf. mean of Poisson distribution)
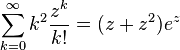 (cf. second moment of Poisson distribution)
(cf. second moment of Poisson distribution)
where  is the Touchard polynomials.
is the Touchard polynomials.
Trigonometric, inverse trigonometric, hyperbolic, and inverse hyperbolic functions
Modified-factorial denominators
Binomial coefficients
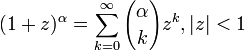 (see Binomial theorem)
(see Binomial theorem)- [2]
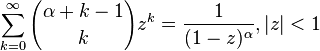
- [2]
 , generating function of the Catalan numbers
, generating function of the Catalan numbers
- [2]
 , generating function of the Central binomial coefficients
, generating function of the Central binomial coefficients
Harmonic numbers
Binomial coefficients
 (see Multiset)
(see Multiset)
 (see Vandermonde identity)
(see Vandermonde identity)
Trigonometric functions
Sums of sines and cosines arise in Fourier series.
Rational functions
- An infinite series of any rational function of
 can be reduced to a finite series of polygamma functions, by use of partial fraction decomposition.[6] This fact can also be applied to finite series of rational functions, allowing the result to be computed in constant time even when the series contains a large number of terms.
can be reduced to a finite series of polygamma functions, by use of partial fraction decomposition.[6] This fact can also be applied to finite series of rational functions, allowing the result to be computed in constant time even when the series contains a large number of terms.
See also
Notes
- ↑ 1.0 1.1 1.2 1.3 generatingfunctionology
- ↑ 2.0 2.1 2.2 2.3 Theoretical computer science cheat sheet
- ↑ "Bernoulli polynomials: Series representations (subsection 06/02)". Retrieved 2 June 2011.
- ↑ Hofbauer, Josef. "A simple proof of 1+1/2^2+1/3^2+...=PI^2/6 and related identities". Retrieved 2 June 2011.
- ↑ Weisstein, Eric W., "Riemann Zeta Function" from MathWorld, equation 52
- ↑ Abramowitz and Stegun
References
- Many books with a list of integrals also have a list of series.
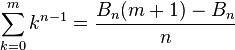


![\sum_{k=1}^m k^3
=\left[\frac{m(m+1)}{2}\right]^2=\frac{m^4}{4}+\frac{m^3}{2}+\frac{m^2}{4}\,\!](../I/m/72a7fa04382ec51d74563b30e028e9e0.png)





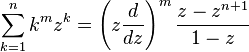

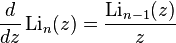
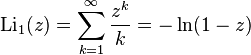
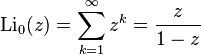

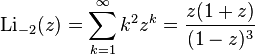



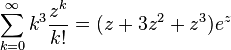


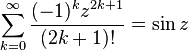

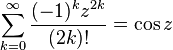


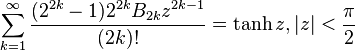





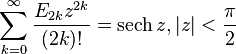







![\sum^{\infty}_{n=0} \frac{\prod_{k=0}^{n-1}(4k^2+\alpha^2)}{(2n)!} z^{2n} + \sum^{\infty}_{n=0} \frac{\alpha \prod_{k=0}^{n-1}[(2k+1)^2+\alpha^2]}{(2n+1)!} z^{2n+1} = e^{\alpha \arcsin{z}}, |z|\le1](../I/m/97888aec56a6f8924ab6a5c48ebe8370.png)


![\sum_{k=1}^\infty \frac{H_k}{k+1} z^{k+1} = \frac{1}{2}\left[\ln(1-z)\right]^2, \qquad |z|<1](../I/m/076d09bd4552c85323ee9daba58fe624.png)


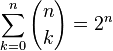



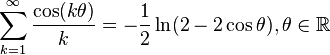
![\sum_{k=0}^\infty \frac{\sin[(2k+1)\theta]}{2k+1}=\frac{\pi}{4}, 0<\theta<\pi\,\!](../I/m/8d53187434d8c0d821d2407ee862f061.png)