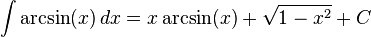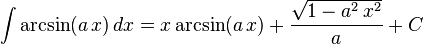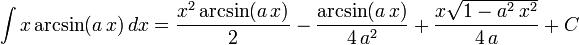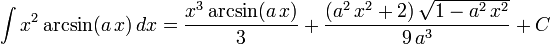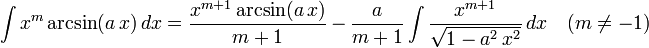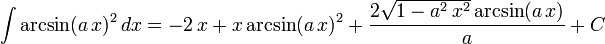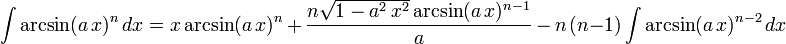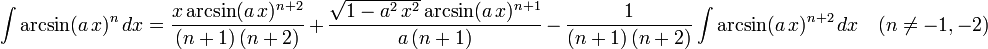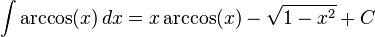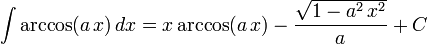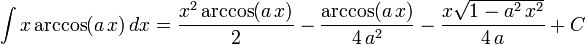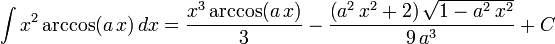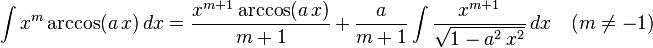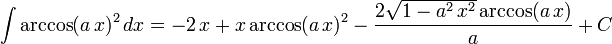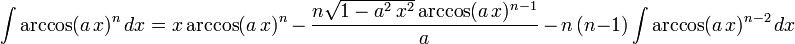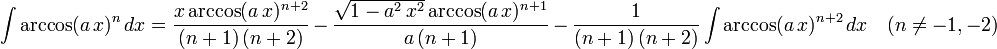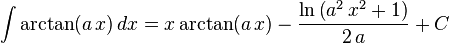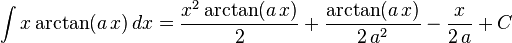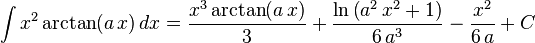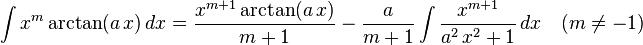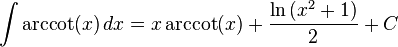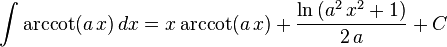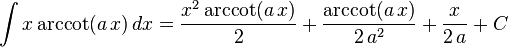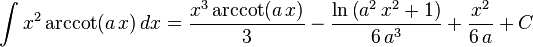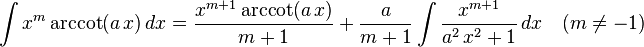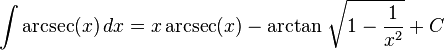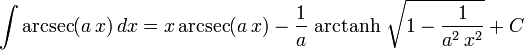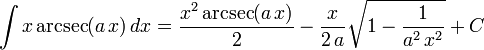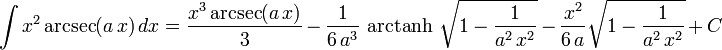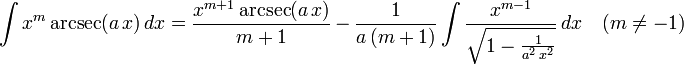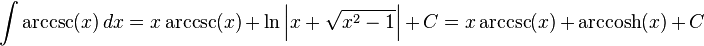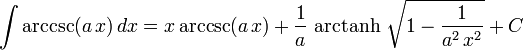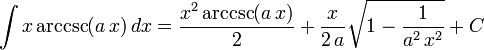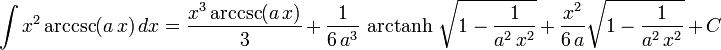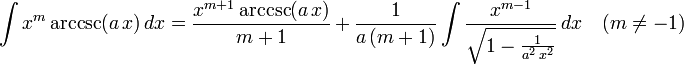List of integrals of inverse trigonometric functions
| Trigonometry |
|---|
| Reference |
| Laws and theorems |
| Calculus |
The following is a list of indefinite integrals (antiderivatives) of expressions involving the inverse trigonometric functions. For a complete list of integral formulas, see lists of integrals.
- The inverse trigonometric functions are also known as the "arc functions".
- C is used for the arbitrary constant of integration that can only be determined if something about the value of the integral at some point is known. Thus each function has an infinite number of antiderivatives.
- There are three common notations for inverse trigonometric functions. The arcsine function, for instance, could be written as sin−1, asin, or, as is used on this page, arcsin.
- For each inverse trigonometric integration formula below there is a corresponding formula in the list of integrals of inverse hyperbolic functions.