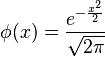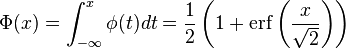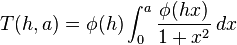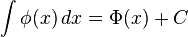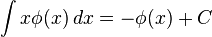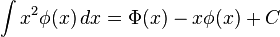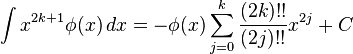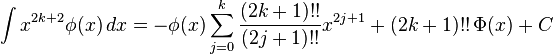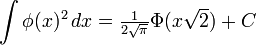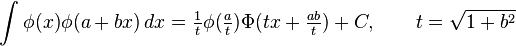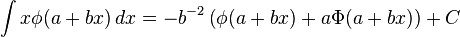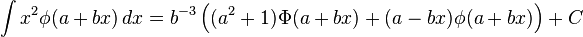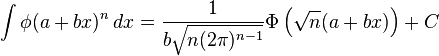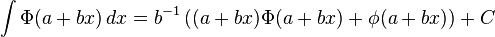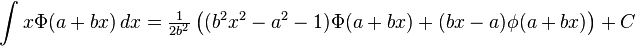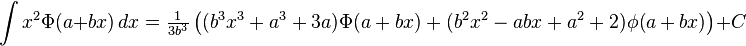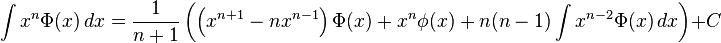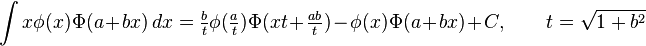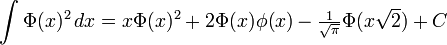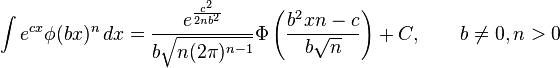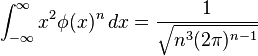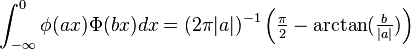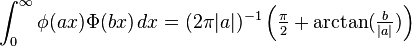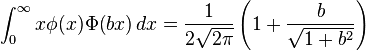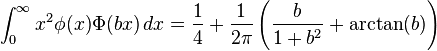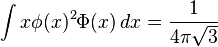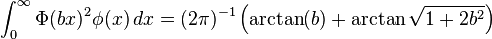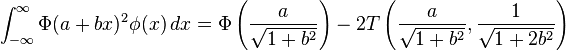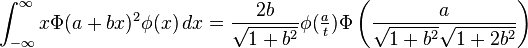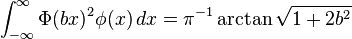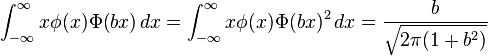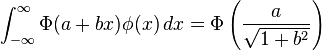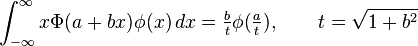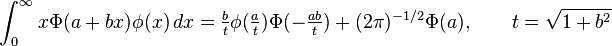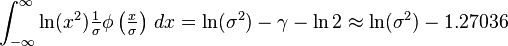List of integrals of Gaussian functions

In these expressions

\phi(x) = \frac{e^{-\frac{x^2}{2}}}{\sqrt{2\pi}}

is the standard normal probability density function,

\Phi(x) = \int_{-\infty}^x \phi(t)dt = \frac12\left(1 + \operatorname{erf}\left(\frac{x}{\sqrt{2}}\right)\right)

is the corresponding cumulative distribution function (where erf is the error function) and

T(h,a) = \phi(h)\int_0^a \frac{\phi(hx)}{1+x^2} \, dx

which is known as the Owen's T function.

Owen [nb 1] has an extensive list of Gaussian-type integrals; only a subset is given below.

Indefinite integrals

\int \phi(x) \, dx = \Phi(x) + C
\int x \phi(x) \, dx = -\phi(x) + C
\int x^2 \phi(x) \, dx = \Phi(x) - x\phi(x) + C
\int x^{2k+1} \phi(x) \, dx = -\phi(x) \sum_{j=0}^k \frac{(2k)!!}{(2j)!!}x^{2j} + C[nb 2]
\int x^{2k+2} \phi(x) \, dx = -\phi(x)\sum_{j=0}^k\frac{(2k+1)!!}{(2j+1)!!}x^{2j+1} + (2k+1)!!\,\Phi(x) + C

In these integrals, n!! is the double factorial: for even n’s it is equal to the product of all even numbers from 2 to n, and for odd n’s it is the product of all odd numbers from 1 to n, additionally it is assumed that 0!! = (−1)!! = 1.

\int \phi(x)^2 \, dx = \tfrac{1}{2\sqrt{\pi}} \Phi(x\sqrt{2}) + C
\int \phi(x)\phi(a + bx) \, dx = \tfrac{1}{t}\phi(\tfrac{a}{t})\Phi(tx + \tfrac{ab}{t}) + C, \qquad t = \sqrt{1+b^2}[nb 3]
\int x\phi(a+bx) \, dx = -b^{-2}\left (\phi(a+bx) + a\Phi(a+bx)\right) + C
\int x^2\phi(a+bx) \, dx = b^{-3} \left ((a^2+1)\Phi(a+bx) + (a-bx)\phi(a+bx) \right ) + C
\int \phi(a+bx)^n \, dx = \frac{1}{b\sqrt{n(2\pi)^{n-1}}} \Phi\left(\sqrt{n}(a+bx)\right) + C
\int \Phi(a+bx) \, dx = b^{-1} \left ((a+bx)\Phi(a+bx) + \phi(a+bx)\right) + C
\int x\Phi(a+bx) \, dx = \tfrac{1}{2b^2}\left((b^2x^2 - a^2 - 1)\Phi(a+bx) + (bx-a)\phi(a+bx)\right) + C
\int x^2\Phi(a+bx) \, dx = \tfrac{1}{3b^3}\left((b^3x^3 + a^3 + 3a)\Phi(a+bx) + (b^2x^2-abx+a^2+2)\phi(a+bx)\right) + C
\int x^n \Phi(x) \, dx = \frac{1}{n+1}\left( \left (x^{n+1}-nx^{n-1} \right )\Phi(x) + x^n\phi(x) + n(n-1)\int x^{n-2}\Phi(x)\,dx \right) + C
\int x\phi(x)\Phi(a+bx) \, dx = \tfrac{b}{t}\phi(\tfrac{a}{t})\Phi(xt + \tfrac{ab}{t}) - \phi(x)\Phi(a+bx) + C, \qquad t = \sqrt{1+b^2}
\int \Phi(x)^2 \, dx = x \Phi(x)^2 + 2\Phi(x)\phi(x) - \tfrac{1}{\sqrt{\pi}}\Phi(x\sqrt{2}) + C
\int e^{cx}\phi(bx)^n \, dx = \frac{e^{\frac{c^2}{2nb^2}}}{b\sqrt{n(2\pi)^{n-1}}}\Phi \left (\frac{b^2xn-c }{b\sqrt{n}} \right ) + C, \qquad b\ne 0, n>0

Definite integrals

\int_{-\infty}^\infty x^2\phi(x)^n \, dx = \frac{1}{\sqrt{n^3(2\pi)^{n-1}}}
\int_{-\infty}^0 \phi(ax)\Phi(bx)dx = (2\pi |a|)^{-1}\left(\tfrac{\pi}{2}-\arctan(\tfrac{b}{|a|})\right)
\int_0^{\infty} \phi(ax)\Phi(bx) \, dx = (2\pi |a|)^{-1}\left(\tfrac{\pi}{2} + \arctan(\tfrac{b}{|a|})\right)
\int_0^\infty x\phi(x)\Phi(bx) \, dx = \frac{1}{2\sqrt{2\pi}} \left( 1 + \frac{b}{\sqrt{1+b^2}} \right)
\int_0^\infty x^2\phi(x)\Phi(bx) \, dx = \frac{1}{4} + \frac{1}{2\pi} \left(\frac{b}{1+b^2} + \arctan(b) \right)
\int x \phi(x)^2\Phi(x) \, dx = \frac{1}{4\pi\sqrt{3}}
\int_0^\infty \Phi(bx)^2 \phi(x) \, dx = (2\pi)^{-1}\left( \arctan(b) + \arctan \sqrt{1+2b^2} \right)
\int_{-\infty}^\infty \Phi(a+bx)^2 \phi(x) \,dx = \Phi\left( \frac{a}{\sqrt{1+b^2}} \right)-2T\left( \frac{a}{\sqrt{1+b^2}}, \frac{1}{\sqrt{1+2b^2}} \right)
\int_{-\infty}^{\infty} x \Phi(a+bx)^2 \phi(x) \,dx = \frac{2b}{\sqrt{1+b^2}} \phi(\tfrac{a}{t}) \Phi\left(\frac{a}{\sqrt{1+b^2}\sqrt{1+2b^2}}\right)[nb 4]
\int_{-\infty}^\infty \Phi(bx)^2 \phi(x) \, dx = \pi^{-1}\arctan \sqrt{1+2b^2}
\int_{-\infty}^\infty x\phi(x)\Phi(bx) \, dx = \int_{-\infty}^\infty x\phi(x)\Phi(bx)^2 \, dx = \frac{b}{\sqrt{2\pi(1+b^2)}}
\int_{-\infty}^\infty \Phi(a+bx)\phi(x) \, dx = \Phi\left(\frac{a}{\sqrt{1+b^2}}\right)
\int_{-\infty}^\infty x\Phi(a+bx)\phi(x) \, dx = \tfrac{b}{t}\phi(\tfrac{a}{t}), \qquad t = \sqrt{1+b^2}
\int_0^\infty x\Phi(a+bx)\phi(x) \, dx =\tfrac{b}{t}\phi(\tfrac{a}{t})\Phi(-\tfrac{ab}{t}) + (2\pi)^{-1/2}\Phi(a), \qquad t = \sqrt{1+b^2}
\int_{-\infty}^\infty \ln(x^2) \tfrac{1}{\sigma}\phi\left(\tfrac{x}{\sigma}\right) \, dx = \ln(\sigma^2) - \gamma - \ln 2 \approx \ln(\sigma^2) - 1.27036

References

  1. ↑ Owen (1980)
  2. ↑ Patel & Read (1996) lists this integral above without the minus sign, which is an error. See calculation by WolframAlpha
  3. ↑ Patel & Read (1996) report this integral with error, see WolframAlpha
  4. ↑ Patel & Read (1996) report this integral incorrectly by omitting x from the integrand