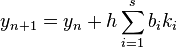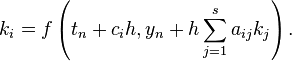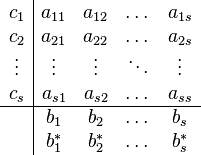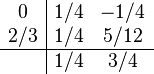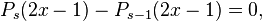List of Runge–Kutta methods
Runge–Kutta methods are methods for the numerical solution of the ordinary differential equation
which take the form
The methods listed on this page are each defined by its Butcher tableau, which puts the coefficients of the method in a table as follows:
Explicit methods
The explicit methods are those where the matrix ![[a_{ij}]](../I/m/58f102d707b5918d8445e64dc0e6db1f.png) is lower triangular.
is lower triangular.
Forward Euler
The Euler method is first order. The lack of stability and accuracy limits its popularity mainly to use as a simple introductory example of a numeric solution method.
Explicit midpoint method
The (explicit) midpoint method is a second-order method with two stages (see also the implicit midpoint method below):
Heun's method
Heun's method is a second-order method with two stages (also known as explicit trapezoid rule):
Ralston's method
Ralston's method is a second-order method with two stages and a minimum local error bound:
Generic second-order method
Kutta's third-order method
Classic fourth-order method
The "original" Runge–Kutta method.
3/8-rule fourth-order method
This method doesn't have as much notoriety as the "classical" method, but is just as classical because it was proposed in the same paper (Kutta, 1901).
Embedded methods
The embedded methods are designed to produce an estimate of the local truncation error of a single Runge-Kutta step, and as result, allow to control the error with adaptive stepsize. This is done by having two methods in the tableau, one with order p and one with order p-1.
The lower-order step is given by
where the 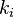 are the same as for the higher order method. Then the error is
are the same as for the higher order method. Then the error is
which is O(h p). The Butcher Tableau for this kind of method is extended to give the values of 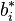
Heun–Euler
The simplest adaptive Runge–Kutta method involves combining Heun's method, which is order 2, with the Euler method, which is order 1. Its extended Butcher Tableau is:
The error estimate is used to control the stepsize.
Bogacki–Shampine
The Bogacki–Shampine method has two methods of orders 3 and 2. Its extended Butcher Tableau is:
| 0 | |||||
| 1/2 | 1/2 | ||||
| 3/4 | 0 | 3/4 | |||
| 1 | 2/9 | 1/3 | 4/9 | ||
| 2/9 | 1/3 | 4/9 | 0 | ||
| 7/24 | 1/4 | 1/3 | 1/8 |
The first row of b coefficients gives the third-order accurate solution, and the second row has order two.
Fehlberg
The Runge–Kutta–Fehlberg method has two methods of orders 5 and 4. Its extended Butcher Tableau is:
| 0 | |||||||
| 1/4 | 1/4 | ||||||
| 3/8 | 3/32 | 9/32 | |||||
| 12/13 | 1932/2197 | −7200/2197 | 7296/2197 | ||||
| 1 | 439/216 | −8 | 3680/513 | −845/4104 | |||
| 1/2 | -8/27 | 2 | −3544/2565 | 1859/4104 | −11/40 | ||
| 16/135 | 0 | 6656/12825 | 28561/56430 | −9/50 | 2/55 | ||
| 25/216 | 0 | 1408/2565 | 2197/4104 | −1/5 | 0 |
The first row of b coefficients gives the fifth-order accurate solution, and the second row has order four.
Cash-Karp
Cash and Karp have modified Fehlberg's original idea. The extended tableau for the Cash–Karp method is
| 0 | |||||||
| 1/5 | 1/5 | ||||||
| 3/10 | 3/40 | 9/40 | |||||
| 3/5 | 3/10 | −9/10 | 6/5 | ||||
| 1 | −11/54 | 5/2 | −70/27 | 35/27 | |||
| 7/8 | 1631/55296 | 175/512 | 575/13824 | 44275/110592 | 253/4096 | ||
| 37/378 | 0 | 250/621 | 125/594 | 0 | 512/1771 | ||
| 2825/27648 | 0 | 18575/48384 | 13525/55296 | 277/14336 | 1/4 |
The first row of b coefficients gives the fifth-order accurate solution, and the second row has order four.
Dormand–Prince
The extended tableau for the Dormand–Prince method is
| 0 | ||||||||
| 1/5 | 1/5 | |||||||
| 3/10 | 3/40 | 9/40 | ||||||
| 4/5 | 44/45 | −56/15 | 32/9 | |||||
| 8/9 | 19372/6561 | −25360/2187 | 64448/6561 | −212/729 | ||||
| 1 | 9017/3168 | −355/33 | 46732/5247 | 49/176 | −5103/18656 | |||
| 1 | 35/384 | 0 | 500/1113 | 125/192 | −2187/6784 | 11/84 | ||
| 35/384 | 0 | 500/1113 | 125/192 | −2187/6784 | 11/84 | 0 | ||
| 5179/57600 | 0 | 7571/16695 | 393/640 | −92097/339200 | 187/2100 | 1/40 |
The first row of b coefficients gives the fifth-order accurate solution, and the second row has order four.
Implicit methods
Backward Euler
The backward Euler method is first order. Unconditionally stable and non-oscillatory for linear diffusion problems.
Implicit midpoint
The implicit midpoint method is of second order. It is the simplest method in the class of collocation methods known as the Gauss methods. It is a symplectic integrator.
Gauss–Legendre methods
These methods are based on the points of Gauss–Legendre quadrature. The Gauss–Legendre method of order four has Butcher tableau:
The Gauss–Legendre method of order six has Butcher tableau:
Lobatto methods
There are three families of Lobatto methods, called IIIA, IIIB and IIIC. These are named after Rehuel Lobatto. All are implicit methods, have order 2s − 2 and they all have c1 = 0 and cs = 1. Unlike any explicit method, it's possible for these methods to have the order greater than the number of stages. Lobatto lived before the classic fourth-order method was popularized by Runge and Kutta.
Lobatto IIIA methods
The Lobatto IIIA methods are collocation methods. The second-order method is known as the trapezoidal rule:
The fourth-order method is given by
Lobatto IIIB methods
The Lobatto IIIB methods are not collocation methods, but they can be viewed as discontinuous collocation methods (Hairer, Lubich & Wanner 2006, §II.1.4). The second-order method is given by
The fourth-order method is given by
Lobatto IIIC methods
The Lobatto IIIC methods also are discontinuous collocation methods. The second-order method is given by
The fourth-order method is given by
Radau methods
Radau methods are fully implicit methods (matrix A of such methods can have any structure). Radau methods attain order 2s − 1 for s stages. Radau methods are A-stable, but expensive to implement. Also they can suffer from order reduction. The first order Radau method is similar to backward Euler method.
Radau IA methods
The third-order method is given by
The fifth-order method is given by
Radau IIA methods
The ci of this method are zeros of
where 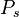 is the Legendre polynomial of degree s.
The third-order method is given by
is the Legendre polynomial of degree s.
The third-order method is given by
The fifth-order method is given by
References
- Hairer, Ernst; Nørsett, Syvert Paul; Wanner, Gerhard (1993), Solving ordinary differential equations I: Nonstiff problems, Berlin, New York: Springer-Verlag, ISBN 978-3-540-56670-0.
- Hairer, Ernst; Wanner, Gerhard (1996), Solving ordinary differential equations II: Stiff and differential-algebraic problems, Berlin, New York: Springer-Verlag, ISBN 978-3-540-60452-5.
- Hairer, Ernst; Lubich, Christian; Wanner, Gerhard (2006), Geometric Numerical Integration: Structure-Preserving Algorithms for Ordinary Differential Equations (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-30663-4.
| |||||||||||||