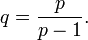List of Banach spaces

In the mathematical field of functional analysis, Banach spaces are among the most important objects of study. In other areas of mathematical analysis, most spaces which arise in practice turn out to be Banach spaces as well.

Classical Banach spaces

According to Diestel (1984, Chapter VII), the classical Banach spaces are those defined by Dunford & Schwartz (1958), which is the source for the following table.

Here K denotes the field of real numbers or complex numbers and I is a closed and bounded interval [a,b]. The number p is a real number with 1 < p < ∞, and q is its Hölder conjugate (also with 1 < q < ∞), so that the next equation holds:

\frac{1}{q}+\frac{1}{p}=1 ,

and thus

q=\frac{p}{p-1} .

The symbol Σ denotes a σ-algebra of sets, and Ξ denotes just an algebra of sets (for spaces only requiring finite additivity, such as the ba space). The symbol μ denotes a positive measure: that is, a real-valued positive set function defined on a σ-algebra which is countably additive.

Classical Banach spaces
Dual space Reflexive weakly complete Norm Notes
Kn Kn Yes Yes \|x\|_2 = \left(\sum_{i=1}^n |x_i|^2\right)^{1/2}
ℓnp ℓnq Yes Yes 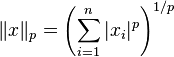\|x\|_p = \left(\sum_{i=1}^n |x_i|^p\right)^{1/p}
ℓn∞ ℓn1 Yes Yes 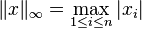\|x\|_\infty = \max_{1\le i\le n} |x_i|
ℓp ℓq Yes Yes 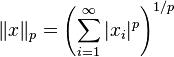\|x\|_p = \left(\sum_{i=1}^\infty |x_i|^p\right)^{1/p} 1 < p < ∞
ℓ1 ℓ∞ No Yes 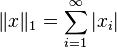\|x\|_1 = \sum_{i=1}^\infty |x_i|
ℓ∞ ba No No 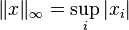\|x\|_\infty = \sup_i |x_i|
c ℓ1 No No 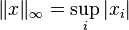\|x\|_\infty = \sup_i |x_i|
c0 ℓ1 No No 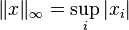\|x\|_\infty = \sup_i |x_i| Isomorphic but not isometric to c.
bv ℓ1 + K No Yes 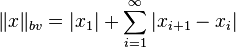\|x\|_{bv} = |x_1| + \sum_{i=1}^\infty|x_{i+1}-x_i|
bv0 ℓ1 No Yes 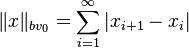\|x\|_{bv_0} = \sum_{i=1}^\infty|x_{i+1}-x_i|
bs ba No No \|x\|_{bs} = \sup_n\left|\sum_{i=1}^nx_i\right| Isometrically isomorphic to ℓ∞.
cs ℓ1 No No \|x\|_{bs} = \sup_n\left|\sum_{i=1}^nx_i\right| Isometrically isomorphic to c.
B(X, Ξ) ba(Ξ) No No \|f\|_B = \sup_{x\in X}|f(x)|
C(X) rca(X) No No \|f\|_{B} = \sup_{x\in X}\left|f(x)\right| X is a compact Hausdorff space.
ba(Ξ) ? No Yes \|\mu\|_{ba} = \sup_{A\in\Sigma} |\mu|(A)

(variation of a measure)
ca(Σ) ? No Yes \|\mu\|_{ba} = \sup_{A\in\Sigma} |\mu|(A)
rca(Σ) ? No Yes \|\mu\|_{ba} = \sup_{A\in\Sigma} |\mu|(A)
Lp(μ) Lq(μ) Yes Yes 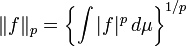\|f\|_p = \left\{\int |f|^p\,d\mu\right\}^{1/p} 1 < p < ∞
L1(μ) L∞(μ) No ? 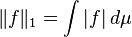\|f\|_1 = \int |f|\,d\mu If the measure μ on S is sigma-finite
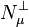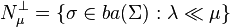L∞(μ) N_\mu^\perp No ? \|f\|_\infty \equiv \inf \{ C\ge 0 : |f(x)| \le C \mbox{ for almost every } x\}. where N_\mu^\perp =\{\sigma\in ba(\Sigma) : \lambda \ll \mu\}
BV(I) ? No Yes 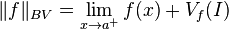\|f\|_{BV} = \lim_{x\to a^+}f(x) + V_f(I) Vf(I) is the total variation of f.
NBV(I) ? No Yes 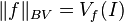\|f\|_{BV} = V_f(I) NBV(I) consists of BV functions such that \lim_{x\to a^+}f(x)=0.
AC(I) K+L∞(I) No Yes 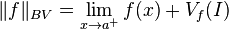\|f\|_{BV} = \lim_{x\to a^+}f(x) + V_f(I) Isomorphic to the Sobolev space W1,1(I).
Cn[a,b] rca([a,b]) No No \|f\| = \sum_{i=0}^n \sup_{x\in [a,b]} |f^{(i)}(x)|. Isomorphic to Rn ⊕ C([a,b]), essentially by Taylor's theorem.


Banach spaces in other areas of analysis

Banach spaces serving as counterexamples

Notes

  1. ↑ W.T. Gowers, "A solution to the Schroeder–Bernstein problem for Banach spaces", Bulletin of the London Mathematical Society, 28 (1996) pp. 297–304.

References