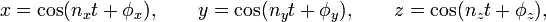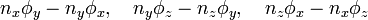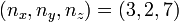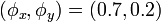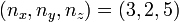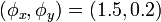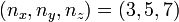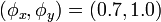Lissajous knot
In knot theory, a Lissajous knot is a knot defined by parametric equations of the form

where 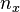 ,
, 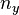 , and
, and 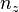 are integers and the phase shifts
are integers and the phase shifts 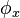 ,
, 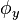 , and
, and 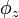 may be any real numbers.[1]
may be any real numbers.[1]
The projection of a Lissajous knot onto any of the three coordinate planes is a Lissajous curve, and many of the properties of these knots are closely related to properties of Lissajous curves.
Replacing the cosine function in the parametrization by a triangle wave transforms every Lissajous knot isotopically into a billiard curve inside a cube, the simplest case of so-called billiard knots. Billiard knots can also be studied in other domains, for instance in a cylinder.[2]
Form
Because a knot cannot be self-intersecting, the three integers 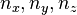 must be pairwise relatively prime, and none of the quantities
must be pairwise relatively prime, and none of the quantities
may be an integer multiple of pi. Moreover, by making a substitution of the form 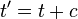 , one may assume that any of the three phase shifts
, one may assume that any of the three phase shifts 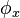 ,
, 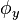 ,
, 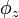 is equal to zero.
is equal to zero.
Examples
Here are some examples of Lissajous knots,[3] all of which have 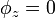 :
:
-

821 knot
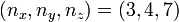
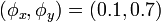
There are infinitely many different Lissajous knots,[4] and other examples with 10 or fewer crossings include the 74 knot, the 815 knot, the 101 knot, the 1035 knot, the 1058 knot, and the composite knot 52* # 52,[1] as well as the 916 knot, 1076 knot, the 1099 knot, the 10122 knot, the 10144 knot, the granny knot, and the composite knot 52 # 52.[5] In addition, it is known that every twist knot with Arf invariant zero is a Lissajous knot.[6]
Symmetry
Lissajous knots are highly symmetric, though the type of symmetry depends on whether or not the numbers 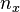 ,
, 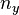 , and
, and 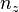 are all odd.
are all odd.
Odd case
If 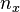 ,
, 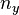 , and
, and 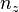 are all odd, then the point reflection across the origin
are all odd, then the point reflection across the origin 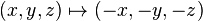 is a symmetry of the Lissajous knot which preserves the knot orientation.
is a symmetry of the Lissajous knot which preserves the knot orientation.
In general, a knot that has an orientation-preserving point reflection symmetry is known as strongly plus amphicheiral.[7] This is a fairly rare property: only three prime knots with twelve or fewer crossings are strongly plus amphicheiral prime knot, the first of which has crossing number ten.[8] Since this is so rare, most Lissajous knots lie in the even case.
Even case
If one of the frequencies (say 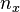 ) is even, then the 180° rotation around the x-axis
) is even, then the 180° rotation around the x-axis 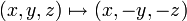 is a symmetry of the Lissajous knot. In general, a knot that has a symmetry of this type is called 2-periodic, so every even Lissajous knot must be 2-periodic.
is a symmetry of the Lissajous knot. In general, a knot that has a symmetry of this type is called 2-periodic, so every even Lissajous knot must be 2-periodic.
Consequences
The symmetry of a Lissajous knot puts severe constraints on the Alexander polynomial. In the odd case, the Alexander polynomial of the Lissajous knot must be a perfect square.[9] In the even case, the Alexander polynomial must be a perfect square modulo 2.[10] In addition, the Arf invariant of a Lissajous knot must be zero. It follows that:
- The trefoil knot and figure-eight knot are not Lissajous.
- No torus knot can be Lissajous.
- No fibered 2-bridge knot can be Lissajous.
References
- ↑ 1.0 1.1 M.G.V. Bogle, J.E. Hearst, V.F.R. Jones, L. Stoilov, "Lissajous knots", Journal of Knot Theory and Its Ramifications, 3(2), 1994, 121–140.
- ↑ C. Lamm, D. Obermeyer. "Billiard knots in a cylinder", Journal of Knot Theory and Its Ramifications, 8(3), 1999, 353–366.
- ↑ Cromwell, Peter R. (2004). Knots and links. Cambridge, UK: Cambridge University Press. p. 13. ISBN 0-521-54831-4.
- ↑ C. Lamm. "There are infinitely many Lissajous knots." Manuscripta Math., 93:29–37, 1997, Springerlink
- ↑ A. Boocher, J. Daigle, J. Hoste, W. Zheng (2007). "Sampling Lissajous and Fourier knots". arXiv:0707.4210.
- ↑ Hoste, Jim; Zirbel, Laura (2006). "Lissajous knots and knots with Lissajous projections". arXiv:math.GT/0605632.
- ↑ Przytycki, Jozef H. (2004). "Symmetric knots and billiard knots". arXiv:math/0405151.
- ↑ Jim Hoste, Morwen Thistlethwaite, and Jeff Weeks. "The first 1,701,936 knots." Math. Intelligencer, 20(4):33–48, 1998.
- ↑ R. Hartley and A Kawauchi. "Polynomials of amphicheiral knots." Math. Ann., 243:63–70, 1979.
- ↑ K. Murasugi. "On periodic knots." Comment. Math.Helv., 46:162–174, 1971.