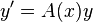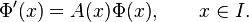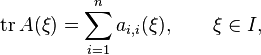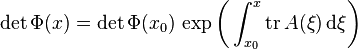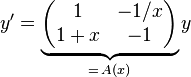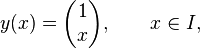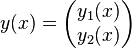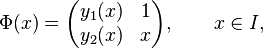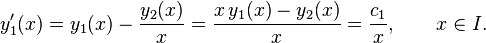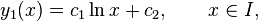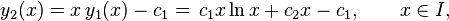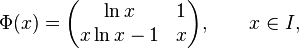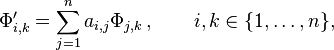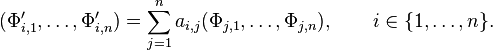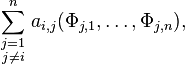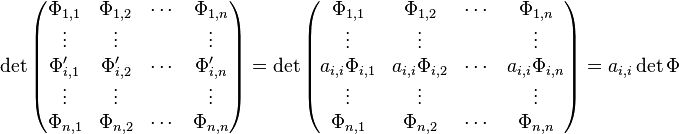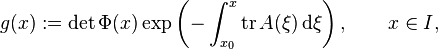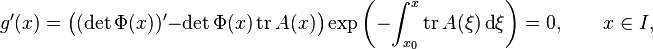Liouville's formula

In mathematics, Liouville's formula, also known as the Abel-Jacobi-Liouville Identity, is an equation that expresses the determinant of a square-matrix solution of a first-order system of homogeneous linear differential equations in terms of the sum of the diagonal coefficients of the system. The formula is named after the French mathematician Joseph Liouville. Jacobi's formula provides another representation of the same mathematical relationship.

Liouville's formula is a generalization of Abel's identity and can be used to prove it. Since Liouville's formula relates the different linearly independent solutions of the system of differential equations, it can help to find one solution from the other(s), see the example application below.

Statement of Liouville's formula

Consider the $n$ -dimensional first-order homogeneous linear differential equation

y'=A(x)y\,

on an interval $I$ of the real line, where $A (x)$ for $x \in I$ denotes a square matrix of dimension $n$ with real or complex entries. Let $Φ$ denote a matrix-valued solution on $I$ , meaning that each $Φ(x)$ is a square matrix of dimension $n$ with real or complex entries and the derivative satisfies

\Phi'(x)=A(x)\Phi(x),\qquad x\in I.

Let

\mathrm{tr}\,A(\xi)=\sum_{i=1}^n a_{i,i}(\xi),\qquad \xi\in I,

denote the trace of $A (ξ) = (a i, j (ξ)) i, j \in {1,..., n}$ , the sum of its diagonal entries. If the trace of $A$ is a continuous function, then the determinant of $Φ$ satisfies

\det\Phi(x)=\det\Phi(x_0)\,\exp\biggl(\int_{x_0}^x \mathrm{tr}\,A(\xi) \,\textrm{d}\xi\biggr)

for all $x$ and $x 0$ in $I$ .

Example application

This example illustrates how Liouville's formula can help to find the general solution of a first-order system of homogeneous linear differential equations. Consider

y'=\underbrace{\begin{pmatrix}1&-1/x\\1+x&-1\end{pmatrix}}_{=\,A(x)}y

on the open interval $I =$ $(0, \infty)$ . Assume that the easy solution

y(x)=\begin{pmatrix}1\\x\end{pmatrix},\qquad x\in I,

is already found. Let

y(x)=\begin{pmatrix}y_1(x)\\y_2(x)\end{pmatrix}

denote another solution, then

\Phi(x)=\begin{pmatrix}y_1(x)&1\\y_2(x)&x\end{pmatrix},\qquad x\in I,

is a square-matrix-valued solution of the above differential equation. Since the trace of $A (x)$ is zero for all $x \in I$ , Liouville's formula implies that the determinant

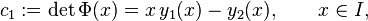
$c_1:=\det\Phi(x)=x\,y_1(x)-y_2(x),\qquad x\in I,$

(1)

is actually a constant independent of $x$ . Writing down the first component of the differential equation for $y$ , we obtain using (1) that

y'_1(x)=y_1(x)-\frac{y_2(x)}x=\frac{x\,y_1(x)-y_2(x)}x=\frac{c_1}x,\qquad x\in I.

Therefore, by integration, we see that

y_1(x)=c_1\ln x+c_2,\qquad x\in I,

involving the natural logarithm and the constant of integration $c 2$ . Solving equation (1) for $y 2 (x)$ and substituting for $y 1 (x)$ gives

y_2(x)=x\,y_1(x)-c_1=\,c_1x\ln x+c_2x-c_1,\qquad x\in I,

which is the general solution for $y$ . With the special choice $c 1 = 0$ and $c 2 = 1$ we recover the easy solution we started with, the choice $c 1 = 1$ and $c 2 = 0$ yields a linearly independent solution. Therefore,

\Phi(x)=\begin{pmatrix}\ln x&1\\x\ln x-1&x\end{pmatrix},\qquad x\in I,

is a so-called fundamental solution of the system.

Proof of Liouville's formula

We omit the argument $x$ for brevity. By the Leibniz formula for determinants, the derivative of the determinant of $Φ = (Φ i, j) i, j \in {0,..., n}$ can be calculated by differentiating one row at a time and taking the sum, i.e.

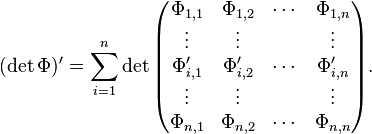
$(\det\Phi)'=\sum_{i=1}^n\det\begin{pmatrix} \Phi_{1,1}&\Phi_{1,2}&\cdots&\Phi_{1,n}\\ \vdots&\vdots&&\vdots\\ \Phi'_{i,1}&\Phi'_{i,2}&\cdots&\Phi'_{i,n}\\ \vdots&\vdots&&\vdots\\ \Phi_{n,1}&\Phi_{n,2}&\cdots&\Phi_{n,n} \end{pmatrix}.$

(2)

Since the matrix-valued solution $Φ$ satisfies the equation $Φ' = A Φ$ , we have for every entry of the matrix $Φ'$

\Phi'_{i,k}=\sum_{j=1}^n a_{i,j}\Phi_{j,k}\,,\qquad i,k\in\{1,\ldots,n\},

or for the entire row

(\Phi'_{i,1},\dots,\Phi'_{i,n}) =\sum_{j=1}^n a_{i,j}(\Phi_{j,1},\ldots,\Phi_{j,n}), \qquad i\in\{1,\ldots,n\}.

When we subtract from the $i$ ^th row the linear combination

\sum_{\scriptstyle j=1\atop\scriptstyle j\not=i}^n a_{i,j}(\Phi_{j,1},\ldots,\Phi_{j,n}),

of all the other rows, then the value of the determinant remains unchanged, hence

\det\begin{pmatrix} \Phi_{1,1}&\Phi_{1,2}&\cdots&\Phi_{1,n}\\ \vdots&\vdots&&\vdots\\ \Phi'_{i,1}&\Phi'_{i,2}&\cdots&\Phi'_{i,n}\\ \vdots&\vdots&&\vdots\\ \Phi_{n,1}&\Phi_{n,2}&\cdots&\Phi_{n,n} \end{pmatrix} =\det\begin{pmatrix} \Phi_{1,1}&\Phi_{1,2}&\cdots&\Phi_{1,n}\\ \vdots&\vdots&&\vdots\\ a_{i,i}\Phi_{i,1}&a_{i,i}\Phi_{i,2}&\cdots&a_{i,i}\Phi_{i,n}\\ \vdots&\vdots&&\vdots\\ \Phi_{n,1}&\Phi_{n,2}&\cdots&\Phi_{n,n} \end{pmatrix} =a_{i,i}\det\Phi

for every $i \in {1, . . . , n$ } by the linearity of the determinant with respect to every row. Hence

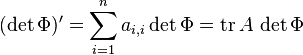
$(\det\Phi)'=\sum_{i=1}^n a_{i,i}\det\Phi=\mathrm{tr}\,A\,\det\Phi$

(3)

by (2) and the definition of the trace. It remains to show that this representation of the derivative implies Liouville's formula.

Fix $x 0 \in I$ . Since the trace of $A$ is assumed to be continuous function on $I$ , it is bounded on every closed and bounded subinterval of $I$ and therefore integrable, hence

g(x):=\det\Phi(x) \exp\left(-\int_{x_0}^x \mathrm{tr}\,A(\xi) \,\textrm{d}\xi\right), \qquad x\in I,

is a well defined function. Differentiating both sides, using the product rule, the chain rule, the derivative of the exponential function and the fundamental theorem of calculus, we obtain

g'(x)=\bigl((\det\Phi(x))'-\det\Phi(x)\,\mathrm{tr}\,A(x)\bigr)\exp\biggl(-\int_{x_0}^x \mathrm{tr}\,A(\xi) \,\textrm{d}\xi\biggr)=0,\qquad x\in I,

due to the derivative in (3). Therefore, $g$ has to be constant on $I$ , because otherwise we would obtain a contradiction to the mean value theorem (applied separately to the real and imaginary part in the complex-valued case). Since $g (x 0) = det Φ(x 0)$ , Liouville's formula follows by solving the definition of $g$ for $det Φ(x)$ .

References

Chicone, Carmen (2006), Ordinary Differential Equations with Applications (2 ed.), New York: Springer-Verlag, pp. 152–153, ISBN 978-0-387-30769-5, MR 2224508, Zbl 1120.34001
Teschl, Gerald (2012), Ordinary Differential Equations and Dynamical Systems, Providence: American Mathematical Society, MR 2961944, Zbl 06054089