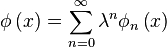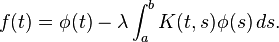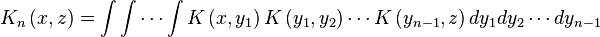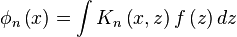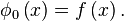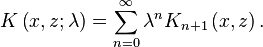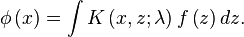Liouville–Neumann series
In mathematics, the Liouville–Neumann series is an infinite series that corresponds to the resolvent formalism technique of solving the Fredholm integral equations in Fredholm theory.
Definition
The Liouville–Neumann series is defined as
which is a unique, continuous solution of a Fredholm integral equation of the second kind:
If the nth iterated kernel is defined as
then
with
The resolvent or solving kernel is given by
The solution of the integral equation becomes
Similar methods may be used to solve the Volterra equations.