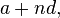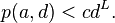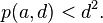Linnik's theorem

Linnik's theorem in analytic number theory answers a natural question after Dirichlet's theorem on arithmetic progressions. It asserts that there exist positive c and L such that, if we denote p(a,d) the least prime in the arithmetic progression

a + nd,\

where n runs through the positive integers and a and d are any given positive coprime integers with 1 ≤ a ≤ d - 1, then:

p(a,d) < c d^{L}. \;

The theorem is named after Yuri Vladimirovich Linnik, who proved it in 1944.[1][2] Although Linnik's proof showed c and L to be effectively computable, he provided no numerical values for them.

Properties

It is known that L ≤ 2 for almost all integers d.[3]

On the generalized Riemann hypothesis it can be shown that

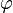p(a,d) \leq (1+o(1))\varphi(d)^2 \ln^2 d \; ,

where \varphi is the totient function.[4]

It is also conjectured that:

p(a,d) < d^2. \; [4]


Bounds for L

The constant L is called Linnik's constant [5] and the following table shows the progress that has been made on determining its size.

L ≤ Year of publication Author
10000 1957 Pan[6]
5448 1958 Pan
777 1965 Chen[7]
630 1971 Jutila
550 1970 Jutila[8]
168 1977 Chen[9]
80 1977 Jutila[10]
36 1977 Graham[11]
20 1981 Graham[12] (submitted before Chen's 1979 paper)
17 1979 Chen[13]
16 1986 Wang
13.5 1989 Chen and Liu[14][15]
8 1990 Wang[16]
5.5 1992 Heath-Brown[4]
5.2 2009 Xylouris[17]
5 2011 Xylouris[18]

Moreover, in Heath-Brown's result the constant c is effectively computable.

Notes

  1. ↑ Linnik, Yu. V. On the least prime in an arithmetic progression I. The basic theorem Rec. Math. (Mat. Sbornik) N.S. 15 (57) (1944), pages 139-178
  2. ↑ Linnik, Yu. V. On the least prime in an arithmetic progression II. The Deuring-Heilbronn phenomenon Rec. Math. (Mat. Sbornik) N.S. 15 (57) (1944), pages 347-368
  3. ↑ E. Bombieri, J. B. Friedlander, H. Iwaniec. "Primes in Arithmetic Progressions to Large Moduli. III", Journal of the American Mathematical Society 2(2) (1989), pp. 215–224.
  4. ↑ 4.0 4.1 4.2 Heath-Brown, D. R. Zero-free regions for Dirichlet L-functions, and the least prime in an arithmetic progression, Proc. London Math. Soc. 64(3) (1992), pp. 265-338
  5. ↑ Guy, Richard K. (1994). Unsolved problems in number theory (2nd ed. ed.). Springer. p. 13. ISBN 0-387-94289-0.
  6. ↑ Pan Cheng Dong On the least prime in an arithmetical progression. Sci. Record (N.S.) 1 (1957) pp. 311-313
  7. ↑ Chen Jingrun On the least prime in an arithmetical progression. Sci. Sinica 14 (1965) pp. 1868-1871
  8. ↑ Jutila, M. A new estimate for Linnik's constant. Ann. Acad. Sci. Fenn. Ser. A I No. 471 (1970) 8 pp.
  9. ↑ Chen Jingrun On the least prime in an arithmetical progression and two theorems concerning the zeros of Dirichlet's $L$-functions. Sci. Sinica 20 (1977), no. 5, pp. 529-562
  10. ↑ Jutila, M. On Linnik's constant. Math. Scand. 41 (1977), no. 1, pp. 45-62
  11. ↑ Applications of sieve methods Ph.D. Thesis, Univ. Michigan, Ann Arbor, Mich., 1977
  12. ↑ Graham, S. W. On Linnik's constant. Acta Arith. 39 (1981), no. 2, pp. 163-179
  13. ↑ Chen Jingrun On the least prime in an arithmetical progression and theorems concerning the zeros of Dirichlet's $L$-functions. II. Sci. Sinica 22 (1979), no. 8, pp. 859-889
  14. ↑ Chen Jingrun and Liu Jian Min On the least prime in an arithmetical progression. III. Sci. China Ser. A 32 (1989), no. 6, pp. 654-673
  15. ↑ Chen Jingrun and Liu Jian Min On the least prime in an arithmetical progression. IV. Sci. China Ser. A 32 (1989), no. 7, pp. 792-807
  16. ↑ Wang On the least prime in an arithmetical progression. Acta Mathematica Sinica, New Series 1991 Vol. 7 No. 3 pp. 279-288
  17. ↑ Triantafyllos Xylouris, On Linnik's constant (2009). arXiv:0906.2749
  18. ↑ Triantafyllos Xylouris, Über die Nullstellen der Dirichletschen L-Funktionen und die kleinste Primzahl in einer arithmetischen Progression (2011). Dr. rer. nat. dissertation.