Link concordance

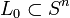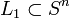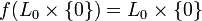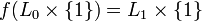In mathematics two links L_0 \subset S^n and L_1 \subset S^n are concordant if there is an embedding f : L_0 \times [0,1] \to S^n \times [0,1] such that f(L_0 \times \{0\}) = L_0 \times \{0\} and f(L_0 \times \{1\}) = L_1 \times \{1\}.

By its nature, link concordance is an equivalence relation. It is weaker than isotopy, and stronger than homotopy: isotopy implies concordance implies homotopy. A link is a slice link if it is concordant to the unlink.

Concordance invariants

A function of a link that is invariant under concordance is called a concordance invariants.

The linking number of any two components of a link is one of the most elementary concordance invariants. The signature of a knot is also a concordance invariant. A subtler concordance invariant are the Milnor invariants, and in fact all rational finite type concordance invariants are Milnor invariants and their products,[1] though non-finite type concordance invariants exist.

Higher dimensions

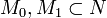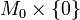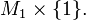
One can analogously define concordance for any two submanifolds M_0, M_1 \subset N. In this case one considers two submanifolds concordant if there is a cobordism between them in N \times [0,1], i.e., if there is a manifold with boundary W \subset N \times [0,1] whose boundary consists of M_0 \times \{0\} and M_1 \times \{1\}.

This higher-dimensional concordance is a relative form of cobordism – it requires two submanifolds to be not just abstractly cobordant, but "cobordant in N".

See also

References

  1. ↑ Habegger, Nathan; Masbaum, Gregor (2000), "The Kontsevich integral and Milnor's invariants", Topology 39 (6): 1253–1289, doi:10.1016/S0040-9383(99)00041-5, preprint.

Further reading