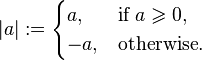Linearly ordered group

In abstract algebra a linearly ordered or totally ordered group is a group G equipped with a total order "≤", that is translation-invariant. This may have different meanings. Let a, b, c ∈ G, we say that (G, ≤) is a

In analogy with ordinary numbers, we call an element c of an ordered group positive if 0 ≤ c and c ≠ 0, where "0" here denotes the identity element of the group (not necessarily the familiar zero of the real numbers). The set of positive elements in a group is often denoted with G+.[1]

For every element a of a linearly ordered group G either a ∈ G+, or -a  ∈ G+, or a = 0. If a linearly ordered group G is not trivial (i.e. 0 is not its only element), then G+ is infinite. Therefore, every nontrivial linearly ordered group is infinite.

If a is an element of a linearly ordered group G, then the absolute value of a, denoted by |a|, is defined to be:

|a|:=\begin{cases}a, & \text{if }a\geqslant0,\\ -a, & \text{otherwise}.\end{cases}

If in addition the group G is abelian, then for any a, b ∈ G the triangle inequality is satisfied: |a + b| ≤ |a| + |b|.

Examples


Any totally ordered group is torsion-free. Conversely, F. W. Levi showed that an abelian group admits a linear order if and only if it is torsion free (Levi 1942).

Otto Hölder showed that every Archimedean group (a bi-ordered group satisfying an Archimedean property) is isomorphic to a subgroup of the additive group of real numbers, (Fuchs & Salce 2001, p. 61). If we write the archimedean l.o. group multiplicatively, this may be shown by considering the dedekind completion, 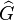\widehat{G} of the closure of an l.o. group under nth roots. 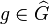We endow this space with the usual topology of a linear order, and then it can be shown that for each g\in\widehat{G} the exponential maps 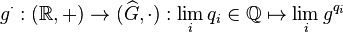g^{\cdot}:(\mathbb{R},+)\to(\widehat{G},\cdot) :\lim_{i}q_{i}\in\mathbb{Q}\mapsto \lim_{i}g^{q_{i}} are well defined order preserving/reversing, topological group isomorphisms. Completing an l.o. group can be difficult in the non-archimedean case. In these cases, one may classify a group by its rank: which is related to the order type of the largest sequence of convex subgroups.

A large source of examples of left-orderable groups comes from groups acting on the real line by order preserving homeomorphisms. Actually, for countable groups, this is known to be a characterization of left-orderability, see for instance (Ghys 2001).

See also

Notes

  1. ↑ Note that the + is written as a subscript, to distinguish from G+ which includes the identity element. See e.g. IsarMathLib, p. 344.

References