Linear phase
Linear phase is a property of a filter, where the phase response of the filter is a linear function of frequency. The result is that all frequency components of the input signal are shifted in time (usually delayed) by the same constant amount, which is referred to as the phase delay. And consequently, there is no phase distortion due to the time delay of frequencies relative to one another.
For discrete-time signals, perfect linear phase is easily achieved with a finite impulse response (FIR) filter. Approximations can be achieved with infinite impulse response (IIR) designs, which are more computationally efficient. Several techniques are:
- a Bessel transfer function which has a maximally flat group delay
- a maximally flat group delay approximation function
- a phase equalizer
Examples
When a sinusoid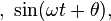 passes through a filter with group delay
passes through a filter with group delay 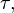 the result is:
the result is:
where:
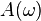 is a frequency-dependent amplitude multiplier.
is a frequency-dependent amplitude multiplier.- The phase shift
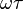 is a linear function of frequency (ω), and
is a linear function of frequency (ω), and 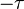 is the slope.
is the slope.
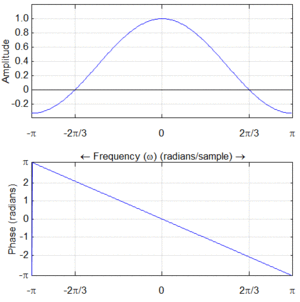
For linear phase, it is sufficient to have that property only in the passband(s) of the filter, where |A(ω)| has relatively large values. Therefore both magnitude and phase graphs (Bode plots) are customarily used to examine a filter's linearity. A "linear" phase graph may contain discontinuities of π and/or 2π radians. The smaller ones happen where A(ω) changes sign. Since |A(ω)| cannot be negative, the changes are reflected in the phase plot. The 2π discontinuities happen because of plotting the principal value of 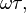 instead of the actual value.
instead of the actual value.
In discrete-time applications, one only examines the region of frequencies between 0 and the Nyquist frequency, because of periodicity and symmetry. Depending on the frequency units, the Nyquist frequency may be 0.5, 1.0, π, or ½ of the actual sample-rate. Some examples of linear and non-linear phase are shown below.
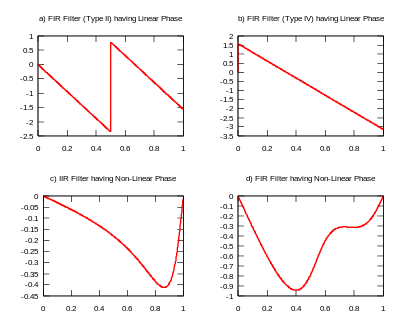

A filter with linear phase may be achieved by an FIR filter which is either symmetric or anti-symmetric.[1] A necessary but not sufficient condition is:
for some 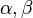 .[2]
.[2]
Generalized linear phase
|
Investigation of potential copyright issue | |
| If you have just labeled this page as a potential copyright issue, please follow the instructions for filing at the bottom of the box. | |
 The previous content of this page or section has been identified as posing a potential copyright issue, as a copy or modification of the text from the source(s) below, and is now listed on Wikipedia:Copyright problems (listing):
Unless the copyright status of the text on this page is clarified, the problematic text or the entire page may be deleted one week after the time of its listing. | |
| Can you help resolve this issue?
If you hold the copyright to this text, you can license it in a manner that allows its use on Wikipedia. Click "Show" to see how.
To demonstrate that this text is in the public domain, or is already under a license suitable for Wikipedia, click "Show".
Explain this on this article's discussion page, with reference to evidence. Wikipedia:Public domain and Wikipedia:Compatibly licensed may assist in determining the status. Otherwise, you may write a new article without copyright-infringing material. Click "Show" to read where and how. Your rewrite should be placed on this page, where it will be available for an administrator or clerk to review it at the end of the listing period. Follow this link to create the temporary subpage.
| |
About importing text to Wikipedia
|
Instructions for filing
If you have tagged the article for investigation, please complete the following steps:
|
See also
Citations
- ↑ Selesnick, Ivan. "Four Types of Linear-Phase FIR Filters". Openstax CNX. Rice University. Retrieved 27 April 2014.
- ↑ Oppenheim, Alan V; Ronald W Schafer (1975). Digital Signal Processing (3 ed.). Prentice Hall. ISBN 0-13-214635-5.
- ↑ Oppenheim, Alan V; Ronald W Schafer (1975). Digital Signal Processing (1 ed.). Prentice Hall. ISBN 0-13-214635-5.
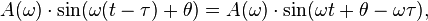
![\sum_{n =-\infty}^\infty h[n] \cdot \sin(\omega \cdot (n - \alpha) + \beta)=0](../I/m/452fc4c50b8c73fe2ddfb5546c0d26f4.png)