Linear Lie algebra

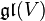In algebra, a linear Lie algebra is a subalgebra $\mathfrak{g}$ of the Lie algebra $\mathfrak{gl}(V)$ consisting of endomorphisms of a vector space V. In other words, a linear Lie algebra is the image of a Lie algebra representation.

Any Lie algebra is a linear Lie algebra in the sense that there is always a faithful representation of $\mathfrak{g}$ (in fact, on a finite-dimensional vector space by Ado's theorem if $\mathfrak{g}$ is itself finite-dimensional.)

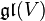Let V be a finite-dimensional vector space over a field of characteristic zero and $\mathfrak{g}$ a subalgebra of $\mathfrak{gl}(V)$ . Then V is semisimple as a module over $\mathfrak{g}$ if and only if (i) it is a direct sum of the center and a semisimple ideal and (ii) the elements of the center are diagonalizable (over some extension field).^[1]

Notes

↑ Jacobson 1962, Ch III, Theorem 10

References

Jacobson, Nathan, Lie algebras, Republication of the 1962 original. Dover Publications, Inc., New York, 1979. ISBN 0-486-63832-4