Limit point compact

In mathematics, a topological space X is said to be limit point compact^[1] or weakly countably compact if every infinite subset of X has a limit point in X. This property generalizes a property of compact spaces. In a metric space, limit point compactness, compactness, and sequential compactness are all equivalent. For general topological spaces, however, these three notions of compactness are not equivalent.

Properties and Examples

• Limit point compactness is equivalent to countable compactness if X is a T₁-space and is equivalent to compactness if X is a metric space.

• An example of a space X that is not weakly countably compact is any countable (or larger) set with the discrete topology. A more interesting example is the countable complement topology.

• Even though a continuous function from a compact space X, to an ordered set Y in the order topology, must be bounded, the same thing does not hold if X is limit point compact. An example is given by the space 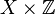(where X = {1, 2} carries the indiscrete topology and 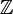is the set of all integers carrying the discrete topology) and the function 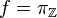given by projection onto the second coordinate. Clearly, ƒ is continuous and 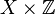is limit point compact (in fact, every nonempty subset of 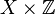has a limit point) but ƒ is not bounded, and in fact 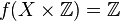is not even limit point compact.

• Every countably compact space (and hence every compact space) is weakly countably compact, but the converse is not true.

• For metrizable spaces, compactness, limit point compactness, and sequential compactness are all equivalent.

• The set of all real numbers, R, is not limit point compact; the integers are an infinite set but do not have a limit point in R.

• If (X, T) and (X, T*) are topological spaces with T* finer than T and (X, T*) is limit point compact, then so is (X, T).

• A finite space is vacuously limit point compact.

See also

• Compact space
• Sequential compactness
• Metric space
• Bolzano-Weierstrass theorem
• Countably compact space

Notes

References

• James Munkres (1999). Topology (2nd edition ed.). Prentice Hall. ISBN 0-13-181629-2. 
• This article incorporates material from Weakly countably compact on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.