Lightface analytic game

In descriptive set theory, a lightface analytic game is a game whose payoff set A is a 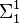$\Sigma^1_1$ subset of Baire space; that is, there is a tree T on 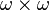$\omega\times\omega$ which is a computable subset of $(\omega\times\omega)^{<\omega}$ , such that A is the projection of the set of all branches of T.

The determinacy of all lightface analytic games is equivalent to the existence of 0^#.