Lie bialgebroid
A Lie bialgebroid is a mathematical structure in the area of non-Riemannian differential geometry. In brief a Lie bialgebroid are two compatible Lie algebroids defined on dual vector bundles. They form the vector bundle version of a Lie bialgebra.
Definition
Preliminary notions
Remember that a Lie algebroid is defined as a skew-symmetric operation [.,.] on the sections Γ(A) of a vector bundle A→M over a smooth manifold M together with a vector bundle morphism ρ: A→TM subject to the Leibniz rule
and Jacobi identity
where Φ, ψk are sections of A and f is a smooth function on M.
The Lie bracket [.,.]A can be extended to multivector fields Γ(⋀A) graded symmetric via the Leibniz rule
for homogeneous multivector fields Φ, Ψ, Χ.
The Lie algebroid differential is an R-linear operator dA on the A-forms ΩA(M) = Γ(⋀A*) of degree 1 subject to the Leibniz-rule
for A-forms α and β. It is uniquely characterized by the conditions
and
for functions f on M, A-1-forms α∈Γ(A*) and Φ, ψ sections of A.
The definition
A Lie bialgebroid are two Lie algebroids (A,ρA,[.,.]A) and (A*,ρ*,[.,.]*) on dual vector bundles A→M and A*→M subject to the compatibility
for all sections Φ, ψ of A. Here d* denotes the Lie algebroid differential of A* which also operates on the multivector fields Γ(∧A).
Symmetry of the definition
It can be shown that the definition is symmetric in A and A*, i.e. (A,A*) is a Lie bialgebroid iff (A*,A) is.
Examples
1. A Lie bialgebra are two Lie algebras (g,[.,.]g) and (g*,[.,.]*) on dual vector spaces g and g* such that the Chevalley–Eilenberg differential δ* is a derivation of the g-bracket.
2. A Poisson manifold (M,π) gives naturally rise to a Lie bialgebroid on TM (with the commutator bracket of tangent vector fields) and T*M with the Lie bracket induced by the Poisson structure. The T*M-differential is d*= [π, .] and the compatibility follows then from the Jacobi-identity of the Schouten bracket.
Infinitesimal version of a Poisson groupoid
It is well known that the infinitesimal version of a Lie groupoid is a Lie algebroid. (As a special case the infinitesimal version of a Lie group is a Lie algebra.) Therefore one can ask which structures need to be differentiated in order to obtain a Lie bialgebroid.
Definition of Poisson groupoid
A Poisson groupoid is a Lie groupoid (G⇉M) together with a Poisson structure π on G such that the multiplication graph m ⊂ G×G×(G,−π) is coisotropic. An example of a Poisson Lie groupoid is a Poisson Lie group (where M=pt, just a point). Another example is a symplectic groupoid (where the Poisson structure is non-degenerate on TG).
Differentiation of the structure
Remember the construction of a Lie algebroid from a Lie groupoid. We take the t-tangent fibers (or equivalently the s-tangent fibers) and consider their vector bundle pulled back to the base manifold M. A section of this vector bundle can be identified with a G-invariant t-vector field on G which form a Lie algebra with respect to the commutator bracket on TG.
We thus take the Lie algebroid A→M of the Poisson groupoid. It can be shown that the Poisson structure induces a fiber-linear Poisson structure on A. Analogous to the construction of the cotangent Lie algebroid of a Poisson manifold there is a Lie algebroid structure on A* induced by this Poisson structure. Analogous to the Poisson manifold case one can show that A and A* form a Lie bialgebroid.
Double of a Lie bialgebroid and superlanguage of Lie bialgebroids
For Lie bialgebroids (g,g*) there is the notion of Manin triples, i.e. c=g+g* can be endowed with the structure of a Lie algebra such that g and g* are subalgebras and c contains the representation of g on g*, vice versa. The sum structure is just
![[X+\alpha,Y+\beta] = [X,Y]_g +\mathrm{ad}_\alpha Y -\mathrm{ad}_\beta X
+[\alpha,\beta]_* +\mathrm{ad}^*_X\beta -\mathrm{ad}^*_Y\alpha](../I/m/d32cab921d9211cbafb53e8a10c66434.png) .
.
Courant algebroids
It turns out that the naive generalization to Lie algebroids does not give a Lie algebroid any more. Instead one has to modify either the Jacobi identity or violate the skew-symmetry and is thus lead to Courant algebroids.[1]
Superlanguage
The appropriate superlanguage of a Lie algebroid A is ΠA, the supermanifold whose space of (super)functions are the A-forms. On this space the Lie algebroid can be encoded via its Lie algebroid differential, which is just an odd vector field.
As a first guess the super-realization of a Lie bialgebroid (A,A*) should be ΠA+ΠA*. But unfortunately dA +d*|ΠA+ΠA* is not a differential, basically because A+A* is not a Lie algebroid. Instead using the larger N-graded manifold T*[2]A[1] = T*[2]A*[1] to which we can lift dA and d* as odd Hamiltonian vector fields, then their sum squares to 0 iff (A,A*) is a Lie bialgebroid.
References
- ↑ Z.-J. Liu, A. Weinstein and P. Xu: Manin triples for Lie bialgebroids, Journ. of diff. geom. vol. 45, pp. 547–574 (1997)
- C. Albert and P. Dazord: Théorie des groupoïdes symplectiques: Chapitre II, Groupoïdes symplectiques. (in Publications du Département de Mathématiques de l’Université Claude Bernard, Lyon I, nouvelle série, pp. 27–99, 1990)
- Y. Kosmann-Schwarzbach: The Lie bialgebroid of a Poisson–Nijenhuis manifold. (Lett. Math. Phys., 38:421–428, 1996)
- K. Mackenzie, P. Xu: Integration of Lie bialgebroids (1997),
- K. Mackenzie, P. Xu: Lie bialgebroids and Poisson groupoids (Duke J. Math, 1994)
- A. Weinstein: Symplectic groupoids and Poisson manifolds (AMS Bull, 1987),
![[\phi,f\cdot\psi] = \rho(\phi)[f]\cdot\psi +f\cdot[\phi,\psi],](../I/m/91d8a58c419a5ba1048889f6965d72ca.png)
![[\phi,[\psi_1,\psi_2]] = [[\phi,\psi_1],\psi_2] +[\psi_1,[\phi,\psi_2]]](../I/m/b5a95eb4127095921b478eaefdf8feb3.png)
![[\Phi\wedge\Psi,\Chi]_A = \Phi\wedge[\Psi,\Chi]_A +(-1)^{|\Psi|(|\Chi|-1)}[\Phi,\Chi]_A\wedge\Psi](../I/m/6c69919ae86b530f1990b8903644a404.png)
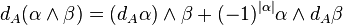
![(d_Af)(\phi) = \rho(\phi)[f]](../I/m/0b11b72d05144df7142ec9611e70ae0a.png)
![(d_A\alpha)[\phi,\psi] = \rho(\phi)[\alpha(\psi)] -\rho(\psi)[\alpha(\phi)] -\alpha[\phi,\psi]](../I/m/0cf25864a475f9d12d4800bb1e354754.png)
![d_*[\phi,\psi]_A = [d_*\phi,\psi]_A +[\phi,d_*\psi]_A](../I/m/51001a487f22de158bc43e2fc7d7bf7d.png)