Lie bialgebra
In mathematics, a Lie bialgebra is the Lie-theoretic case of a bialgebra: it's a set with a Lie algebra and a Lie coalgebra structure which are compatible.
It is a bialgebra where the comultiplication is skew-symmetric and satisfies a dual Jacobi identity, so that the dual vector space is a Lie algebra, whereas the comultiplication is a 1-cocycle, so that the multiplication and comultiplication are compatible. The cocycle condition implies that, in practice, one studies only classes of bialgebras that are cohomologous to a Lie bialgebra on a coboundary.
They are also called Poisson-Hopf algebras, and are the Lie algebra of a Poisson-Lie group.
Lie bialgebras occur naturally in the study of the Yang-Baxter equations.
Definition
A vector space  is a Lie bialgebra if it is a Lie algebra,
and there is the structure of Lie algebra also on the dual vector space
is a Lie bialgebra if it is a Lie algebra,
and there is the structure of Lie algebra also on the dual vector space 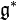 which is compatible.
More precisely the Lie algebra structure on
which is compatible.
More precisely the Lie algebra structure on  is given
by a Lie bracket
is given
by a Lie bracket ![[\ ,\ ]:\mathfrak{g} \otimes \mathfrak{g} \to \mathfrak{g}](../I/m/fb88114e6cf4d6ce9ef98138c9ca79e8.png) and the Lie algebra structure on
and the Lie algebra structure on 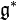 is given by a Lie
bracket
is given by a Lie
bracket 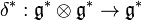 .
Then the map dual to
.
Then the map dual to 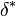 is called the cocommutator,
is called the cocommutator,
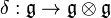 and the compatibility condition is the following cocyle relation:
and the compatibility condition is the following cocyle relation:
where ![\operatorname{ad}_XY=[X,Y]](../I/m/618e0a91b2ab7ac164a43c1621f70cbd.png) is the adjoint.
Note that this definition is symmetric and
is the adjoint.
Note that this definition is symmetric and 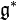 is also a Lie bialgebra, the dual Lie bialgebra.
is also a Lie bialgebra, the dual Lie bialgebra.
Example
Let  be any semisimple Lie algebra.
To specify a Lie bialgebra structure we thus need to specify a compatible Lie algebra structure on the dual vector space.
Choose a Cartan subalgebra
be any semisimple Lie algebra.
To specify a Lie bialgebra structure we thus need to specify a compatible Lie algebra structure on the dual vector space.
Choose a Cartan subalgebra 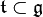 and a choice of positive roots.
Let
and a choice of positive roots.
Let 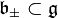 be the corresponding opposite Borel subalgebras, so that
be the corresponding opposite Borel subalgebras, so that 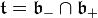 and there is a natural projection
and there is a natural projection 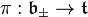 .
Then define a Lie algebra
.
Then define a Lie algebra
which is a subalgebra of the product 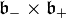 , and has the same dimension as
, and has the same dimension as  .
Now identify
.
Now identify 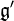 with dual of
with dual of  via the pairing
via the pairing
where 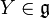 and
and  is the Killing form.
This defines a Lie bialgebra structure on
is the Killing form.
This defines a Lie bialgebra structure on  , and is the "standard" example: it underlies the Drinfeld-Jimbo quantum group.
Note that
, and is the "standard" example: it underlies the Drinfeld-Jimbo quantum group.
Note that 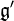 is solvable, whereas
is solvable, whereas  is semisimple.
is semisimple.
Relation to Poisson-Lie groups
The Lie algebra  of a Poisson-Lie group G has a natural structure of Lie bialgebra.
In brief the Lie group structure gives the Lie bracket on
of a Poisson-Lie group G has a natural structure of Lie bialgebra.
In brief the Lie group structure gives the Lie bracket on  as usual, and the linearisation of the Poisson structure on G
gives the Lie bracket on
as usual, and the linearisation of the Poisson structure on G
gives the Lie bracket on
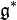 (recalling that a linear Poisson structure on a vector space is the same thing as a Lie bracket on the dual vector space).
In more detail, let G be a Poisson-Lie group, with
(recalling that a linear Poisson structure on a vector space is the same thing as a Lie bracket on the dual vector space).
In more detail, let G be a Poisson-Lie group, with 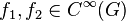 being two smooth functions on the group manifold. Let
being two smooth functions on the group manifold. Let 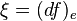 be the differential at the identity element. Clearly,
be the differential at the identity element. Clearly, 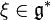 . The Poisson structure on the group then induces a bracket on
. The Poisson structure on the group then induces a bracket on 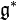 , as
, as
where 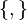 is the Poisson bracket. Given
is the Poisson bracket. Given 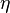 be the Poisson bivector on the manifold, define
be the Poisson bivector on the manifold, define 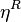 to be the right-translate of the bivector to the identity element in G. Then one has that
to be the right-translate of the bivector to the identity element in G. Then one has that
The cocommutator is then the tangent map:
so that
is the dual of the cocommutator.
See also
References
- H.-D. Doebner, J.-D. Hennig, eds, Quantum groups, Proceedings of the 8th International Workshop on Mathematical Physics, Arnold Sommerfeld Institute, Claausthal, FRG, 1989, Springer-Verlag Berlin, ISBN 3-540-53503-9.
- Vyjayanthi Chari and Andrew Pressley, A Guide to Quantum Groups, (1994), Cambridge University Press, Cambridge ISBN 0-521-55884-0.
![\delta([X,Y]) = \left(
\operatorname{ad}_X \otimes 1 + 1 \otimes \operatorname{ad}_X
\right) \delta(Y) - \left(
\operatorname{ad}_Y \otimes 1 + 1 \otimes \operatorname{ad}_Y
\right) \delta(X)](../I/m/35417ed30a50b976c9bb4f793e1148fd.png)
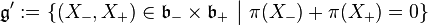
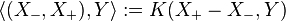
![[\xi_1,\xi_2]=(d\{f_1,f_2\})_e\,](../I/m/2c7d86540e113da19fc5e35acc010422.png)
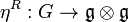
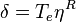
![[\xi_1,\xi_2]= \delta^*(\xi_1 \otimes \xi_2)](../I/m/f41b0b235c0e364e7bd1172824c67a68.png)