Lie algebra bundle
In Mathematics, a weak Lie algebra bundle
is a vector bundle 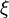 over a base space X together with a morphism
over a base space X together with a morphism
which induces a Lie algebra structure on each fibre 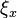 .
.
A Lie algebra bundle 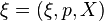 is a vector bundle in which
each fibre is a Lie algebra and for every x in X, there is an open set
is a vector bundle in which
each fibre is a Lie algebra and for every x in X, there is an open set  containing x, a Lie algebra L and a homeomorphism
containing x, a Lie algebra L and a homeomorphism
such that
is a Lie algebra isomorphism.
Any Lie algebra bundle is a weak Lie algebra bundle but the converse need not be true in general.
As an example of a weak Lie algebra bundle that is not a strong Lie algebra bundle, consider the total space 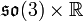 over the real line
over the real line 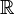 . Let [.,.] denote the Lie bracket of
. Let [.,.] denote the Lie bracket of 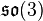 and deform it by the real parameter as:
and deform it by the real parameter as:
for 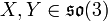 and
and 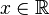 .
.
Lie's third theorem states that every bundle of Lie algebras can locally be integrated to a bundle of Lie groups. However globally the total space might fail to be Hausdorff.[1]
References
- ↑ A. Weinstein, A.C. da Silva: Geometric models for noncommutative algebras, 1999 Berkley LNM, online readable at , in particular chapter 16.3.
- A.Douady et M.Lazard, Espaces fibres en algebre de Lie et en groups, Invent. math., Vol. 1, 1966, pp. 133–151
- B.S.Kiranagi, Lie Algebra bundles, Bull. Sci. Math., 2e serie, 102(1978), 57-62.
- B.S.Kiranagi, Semi simple Lie algebra bundles, Bull. Math de la Sci. Math de la R.S.de Roumaine, 27 (75), 1983, 253-257.
- B.S.Kiranagi and G.Prema, On complete reducibility of Module Bundles, Bull. Austral. Math Soc., 28 (1983), 401-409.
- B.S.Kiranagi and G.Prema, Cohomology of Lie algebra bundles and its applications, Ind. J. Pure and Appli. Math. 16(7): 1985, 731/735.
- B.S.Kiranagi and G.Prema, Lie algebra bundles defined by Jordan algebra bundles, Bull. Math. Soc.Sci.Math.Rep.Soc. Roum., Noun. Ser. 33 (81), 1989, 255-264.
- B.S.Kiranagi and G.Prema, On complete reducibility of Bimodule bundles, Bull. Math. Soc. Sci.Math. Repose; Roum, Nouv.Ser. 33 (81), 1989, 249-255.
- B.S.Kiranagi and G.Prema, A decomposition theorem of Lie algebra Bundles, Communications in Algebra 18 (6), 1990, 1869-1877 .
- B.S.Kiranagi, G.Prema and C.Chidambara, Rigidity theorem for Lie algebra Bundles, Communications in Algebra 20 (6), 1992, pp. 1549 – 1556.
- Kiranagi, B.S.; Ranjitha, Kumar; Prema, G. (2014), "On completely semisimple Lie algebra bundles", Journal of Algebra and its Applications 14 (2): 1–11, doi:10.1142/S0219498815500097.
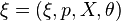
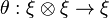
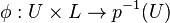
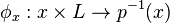
![[X,Y]_x = x\cdot[X,Y]](../I/m/152c8e8539f16f4032ee216cb5d2b181.png)