Lehmann–Scheffé theorem
In statistics, the Lehmann–Scheffé theorem is prominent in mathematical statistics, tying together the ideas of completeness, sufficiency, uniqueness, and best unbiased estimation.[1] The theorem states that any estimator which is unbiased for a given unknown quantity and which is based on only a complete, sufficient statistic (and on no other data-derived values) is the unique best unbiased estimator of that quantity. The Lehmann–Scheffé theorem is named after Erich Leo Lehmann and Henry Scheffé, given their two early papers.[2][3]
If T is a complete sufficient statistic for θ and E(g(T)) = τ(θ) then g(T) is the minimum-variance unbiased estimator (MVUE) of τ(θ).
Statement
Let 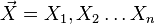 be a random sample from a distribution that has p.d.f (or p.m.f in the discrete case)
be a random sample from a distribution that has p.d.f (or p.m.f in the discrete case) 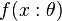 where
where 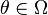 is a parameter in the parameter space. Suppose
is a parameter in the parameter space. Suppose 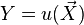 is a sufficient statistic for θ, and let
is a sufficient statistic for θ, and let 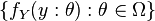 be a complete family. If
be a complete family. If ![\phi:\mathbb{E}[\phi(Y)] = \theta](../I/m/955a12c6d7b6fbdcb4d0673bebc76ac3.png) then
then 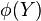 is the unique MVUE of θ.
is the unique MVUE of θ.
Proof
By the Rao–Blackwell theorem, if 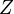 is an unbiased estimator of θ then
is an unbiased estimator of θ then ![\phi(Y):= \mathbb{E}[Z|Y]](../I/m/ead8ac9d2a761cfbd6244cab3c6e1477.png) defines an unbiased estimator of θ with the property that its variance is smaller than that of
defines an unbiased estimator of θ with the property that its variance is smaller than that of 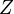 .
.
Now we show that this function is unique. Suppose 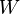 is another candidate MVUE estimator of θ. Then again
is another candidate MVUE estimator of θ. Then again ![\psi(Y):= \mathbb{E}[W|Y]](../I/m/faa45e714922124ca771640fd7b356c4.png) defines an unbiased estimator of θ with the property that its variance is smaller than that of
defines an unbiased estimator of θ with the property that its variance is smaller than that of 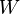 . Then
. Then
Since 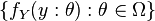 is a complete family
is a complete family
and therefore the function  is the unique function of Y that has a smaller variance than any unbiased estimator. We conclude that
is the unique function of Y that has a smaller variance than any unbiased estimator. We conclude that 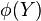 is the MVUE.
is the MVUE.
See also
- Basu's theorem
- Complete class theorem
- Rao–Blackwell theorem
References
- ↑ Casella, George (2001). Statistical Inference. Duxbury Press. p. 369. ISBN 0-534-24312-6.
- ↑ Lehmann, E. L.; Scheffé, H. (1950). "Completeness, similar regions, and unbiased estimation. I.". Sankhyā 10 (4): 305–340. JSTOR 25048038. MR 39201.
- ↑ Lehmann, E.L.; Scheffé, H. (1955). "Completeness, similar regions, and unbiased estimation. II.". Sankhyā 15 (3): 219–236. JSTOR 25048243. MR 72410.
![\mathbb{E}[\phi(Y) - \psi(Y)] = 0, \theta \in \Omega.](../I/m/694fab11c5ba3adb95f2670deb69425c.png)
![\mathbb{E}[\phi(Y) - \psi(Y)] = 0 \implies \phi(y) - \psi(y) = 0, \theta \in \Omega](../I/m/46a399598c2fba48ad808fe297d5d210.png)