Legendrian knot

In mathematics, a Legendrian knot often refers to a smooth embedding of the circle into 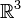$\mathbb R^3$ , which is tangent to the standard contact structure on 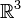$\mathbb R^3$ . It is the lowest-dimensional case of a Legendrian submanifold, which is an embedding of a k-dimensional manifold into a (2k+1)-dimensional that is always tangent to the contact hyperplane.

Two Legendrian knots are equivalent if they are isotopic through a family of Legendrian knots. There can be inequivalent Legendrian knots that are isotopic as topological knots. Many inequivalent Legendrian knots can be distinguished by considering their Thurston-Bennequin invariants and rotation number, which are together known as the "classical invariants" of Legendrian knots. More sophisticated invariants have been constructed, including one constructed combinatorially by Chekanov and using holomorphic discs by Eliashberg. This Chekanov-Eliashberg invariant yields an invariant for loops of Legendrian knots by considering the monodromy of the loops. This has yielded noncontractible loops of Legendrian knots which are contractible in the space of all knots.

Any Legendrian knot may be C^0 perturbed to a transverse knot (a knot transverse to a contact structure) by pushing off in a direction transverse to the contact planes. The set of isomorphism classes of Legendrian knots modulo negative Legendrian stabilizations is in bijection with the set of transverse knots.

References

Geiges, Hansjörg (2008). An introduction to contact topology; Volume 109 of Cambridge studies in advanced mathematics. Cambridge University Press. p. 94. ISBN 0-521-86585-9.
Casacuberta, Carlos (2001). European Congress of Mathematics: Barcelona, July 10–14, 2000,. Birkhäuser. p. 526. ISBN 3764364181.
Epstein, J.; Fuchs, D.; Meyer, M. (2001). "Chekanov–Eliashberg invariants and transverse approximations of Legendrian knots". Pacific Journal of Mathematics 201 (1): 89–106. doi:10.2140/pjm.2001.201.89.
Kalman, Tamas (2005). "Contact homology and one parameter families of Legendrian knots". Geometry & Topology 9: 2013–2078. doi:10.2140/gt.2005.9.2013.
Sabloff, Joshua M. (2009), "What Is . . . a Legendrian Knot?", AMS Notices 56 (10): 1282–1284 .