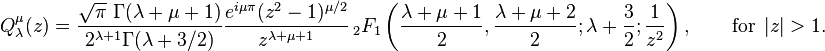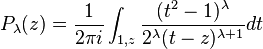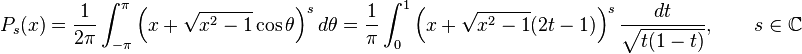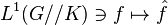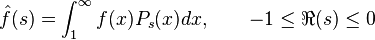Legendre function

For the most common case of integer degree, see Legendre polynomials and associated Legendre polynomials.

In mathematics, the Legendre functions P_λ, Q_λ and associated Legendre functions Pμ
λ, Qμ
λ are generalizations of Legendre polynomials to non-integer degree.

Associated Legendre polynomial curves for l=5.

Differential equation

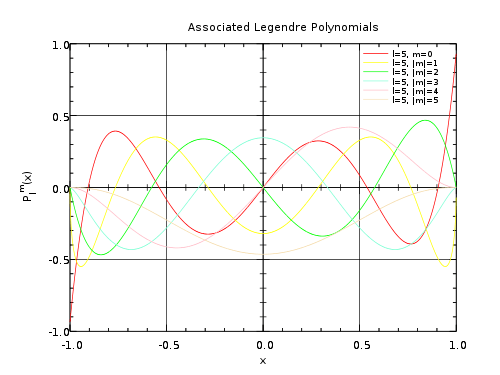
Associated Legendre functions are solutions of the general Legendre equation

(1-x^2)\,y'' -2xy' + \left[\lambda(\lambda+1) - \frac{\mu^2}{1-x^2}\right]\,y = 0,\,

where the complex numbers λ and μ are called the degree and order of the associated Legendre functions, respectively. The Legendre polynomials are the associated Legendre functions of order μ=0.

This is a second order linear equation with three regular singular points (at 1, −1, and ∞). Like all such equations, it can be converted into a hypergeometric differential equation by a change of variable, and its solutions can be expressed using hypergeometric functions.

Definition

These functions may actually be defined for general complex parameters and argument:

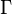P_{\lambda}^{\mu}(z) = \frac{1}{\Gamma(1-\mu)} \left[\frac{1+z}{1-z}\right]^{\mu/2} \,_2F_1 (-\lambda, \lambda+1; 1-\mu; \frac{1-z}{2}),\qquad \text{for } \ |1-z|<2

where $\Gamma$ is the gamma function and 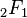$_2F_1$ is the hypergeometric function.

The second order differential equation has a second solution, 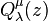$Q_\lambda^{\mu}(z)$ , defined as:

Q_{\lambda}^{\mu}(z) = \frac{\sqrt{\pi}\ \Gamma(\lambda+\mu+1)}{2^{\lambda+1}\Gamma(\lambda+3/2)}\frac{e^{i\mu\pi}(z^2-1)^{\mu/2}}{z^{\lambda+\mu+1}} \,_2F_1 \left(\frac{\lambda+\mu+1}{2}, \frac{\lambda+\mu+2}{2}; \lambda+\frac{3}{2}; \frac{1}{z^2}\right),\qquad \text{for}\ \ |z|>1.

Integral representations

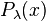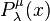The Legendre functions can be written as contour integrals. For example (needs clarification: how is $P_\lambda(x)$ related to $P^\mu_\lambda(x)$ ?)

P_\lambda(z) =\frac{1}{2\pi i} \int_{1,z} \frac{(t^2-1)^\lambda}{2^\lambda(t-z)^{\lambda+1}}dt

where the contour circles around the points 1 and z in the positive direction and does not circle around −1. For real x, we have

P_s(x) = \frac{1}{2\pi}\int_{-\pi}^{\pi}\left(x+\sqrt{x^2-1}\cos\theta\right)^s d\theta = \frac{1}{\pi}\int_0^1\left(x+\sqrt{x^2-1}(2t-1)\right)^s\frac{dt}{\sqrt{t(1-t)}},\qquad s\in\mathbb{C}

Legendre function as characters

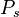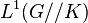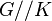The real integral representation of $P_s$ are very useful in the study of harmonic analysis on $L^1(G//K)$ where $G//K$ is the double coset space of 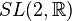$SL(2,\mathbb{R})$ (see Zonal spherical function). Actually the Fourier transform on 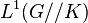$L^1(G//K)$ is given by

L^1(G//K)\ni f\mapsto \hat{f}

where

\hat{f}(s)=\int_1^\infty f(x)P_s(x)dx,\qquad -1\leq\Re(s)\leq 0

References

Abramowitz, Milton; Stegun, Irene A., eds. (1965), "Chapter 8", Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover, p. 332, ISBN 978-0486612720, MR 0167642 .
Courant, Richard; Hilbert, David (1953), Methods of Mathematical Physics, Volume 1, New York: Interscience Publisher, Inc .
Dunster, T. M. (2010), "Legendre and Related Functions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR 2723248
Ivanov, A.B. (2001), "L/l058030", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Snow, Chester (1952) [1942], Hypergeometric and Legendre functions with applications to integral equations of potential theory, National Bureau of Standards Applied Mathematics Series, No. 19, Washington, D.C.: U. S. Government Printing Office, MR 0048145
Whittaker, E. T.; Watson, G. N. (1963), A Course in Modern Analysis, Cambridge University Press, ISBN 978-0-521-58807-2

External links

Legendre function P on the Wolfram functions site.
Legendre function Q on the Wolfram functions site.
Associated Legendre function P on the Wolfram functions site.
Associated Legendre function Q on the Wolfram functions site.