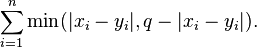Lee distance

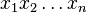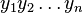In coding theory, the Lee distance is a distance between two strings $x_1 x_2 \dots x_n$ and $y_1 y_2 \dots y_n$ of equal length n over the q-ary alphabet {0, 1, …, q − 1} of size q ≥ 2. It is a metric, defined as

\sum_{i=1}^n \min(|x_i-y_i|,q-|x_i-y_i|).

If q = 2 the Lee distance coincides with the Hamming distance.

The metric space induced by the Lee distance is a discrete analog of the elliptic space.

Example

If q = 6, then the Lee distance between 3140 and 2543 is 1 + 2 + 0 + 3 = 6.

History and application

The Lee distance is named after C. Y. Lee. It is applied for phase modulation while the Hamming distance is used in case of orthogonal modulation.

References

Lee, C. Y. (1958), "Some properties of nonbinary error-correcting codes", IRE Transactions on Information Theory 4 (2): 77–82, doi:10.1109/TIT.1958.1057446 .
Berlekamp, E. R. (1968), Algebraic Coding Theory, McGraw-Hill .
Deza, E.; Deza, M. (2006), Dictionary of Distances, Elsevier, ISBN 0-444-52087-2 .