Lebesgue's number lemma

In topology, Lebesgue's number lemma, named after Henri Lebesgue, is a useful tool in the study of compact metric spaces. It states:

If the metric space (X, d) is compact and an open cover of X is given, then there exists a number δ > 0 such that every subset of X having diameter less than δ is contained in some member of the cover.

Such a number δ is called a Lebesgue number of this cover. The notion of a Lebesgue number itself is useful in other applications as well.

Proof

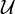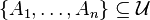Let $\mathcal U$ be an open cover of $X$ . Since $X$ is compact we can extract a finite subcover $\{A_1, \dots, A_n\} \subseteq \mathcal U$ .

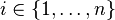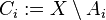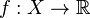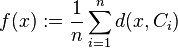For each $i \in \{1, \dots, n\}$ , let $C_i := X \setminus A_i$ and define a function $f : X \rightarrow \mathbb R$ by $f(x) := \frac{1}{n} \sum_{i=1}^n d(x,C_i)$ .

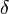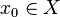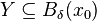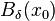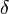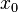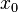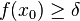Since $f$ is continuous on a compact set, it attains a minimum $\delta$ . The key observation is that $\delta > 0$ . If $Y$ is a subset of $X$ of diameter less than $\delta$ , then there exist $x_0\in X$ such that $Y\subseteq B_\delta(x_0)$ , where $B_\delta(x_0)$ denotes the radius $\delta$ ball centered at $x_0$ (namely, one can choose as $x_0$ any point in $Y$ ). 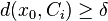Since $f(x_0)\geq \delta$ there must exist at least one $i$ such that $d(x_0,C_i)\geq \delta$ . 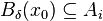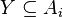But this means that $B_\delta(x_0)\subseteq A_i$ and so, in particular, $Y\subseteq A_i$ .

References

Munkres, James R. (1974), Topology: A first course, p. 179, ISBN 978-0-13-925495-6