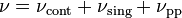Lebesgue's decomposition theorem
In mathematics, more precisely in measure theory, Lebesgue's decomposition theorem[1][2][3] states that for every two σ-finite signed measures  and
and 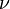 on a measurable space
on a measurable space 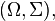 there exist two σ-finite signed measures
there exist two σ-finite signed measures 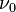 and
and 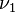 such that:
such that:
-
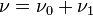
-
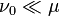 (that is,
(that is, 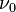 is absolutely continuous with respect to
is absolutely continuous with respect to  )
) -
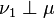 (that is,
(that is, 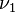 and
and  are singular).
are singular).
These two measures are uniquely determined by  and
and 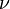 .
.
Refinement
Lebesgue's decomposition theorem can be refined in a number of ways.
First, the decomposition of the singular part of a regular Borel measure on the real line can be refined:[4]
where
- νcont is the absolutely continuous part
- νsing is the singular continuous part
- νpp is the pure point part (a discrete measure).
Second, absolutely continuous measures are classified by the Radon–Nikodym theorem, and discrete measures are easily understood. Hence (singular continuous measures aside), Lebesgue decomposition gives a very explicit description of measures. The Cantor measure (the probability measure on the real line whose cumulative distribution function is the Cantor function) is an example of a singular continuous measure.
Related concepts
Lévy–Itō decomposition
The analogous decomposition for a stochastic processes is the Lévy–Itō decomposition: given a Lévy process X, it can be decomposed as a sum of three independent Lévy processes 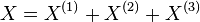 where:
where:
-
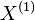 is a Brownian motion with drift, corresponding to the absolutely continuous part;
is a Brownian motion with drift, corresponding to the absolutely continuous part; -
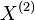 is a compound Poisson process, corresponding to the pure point part;
is a compound Poisson process, corresponding to the pure point part; -
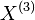 is a square integrable pure jump martingale that almost surely has a countable number of jumps on a finite interval, corresponding to the singular continuous part.
is a square integrable pure jump martingale that almost surely has a countable number of jumps on a finite interval, corresponding to the singular continuous part.
See also
- Decomposition of spectrum
- Hahn decomposition theorem and the corresponding Jordan decomposition theorem
Citations
- ↑ (Halmos 1974, Section 32, Theorem C)
- ↑ (Hewitt & Stromberg 1965, Chapter V, § 19, (19.42) Lebesgue Decomposition Theorem)
- ↑ (Rudin 1974, Section 6.9, The Theorem of Lebesgue-Radon-Nikodym)
- ↑ (Hewitt & Stromberg 1965, Chapter V, § 19, (19.61) Theorem)
References
- Halmos, Paul R. (1974) [1950], Measure Theory, Graduate Texts in Mathematics 18, New York, Heidelberg, Berlin: Springer-Verlag, ISBN 978-0-387-90088-9, MR 0033869, Zbl 0283.28001
- Hewitt, Edwin; Stromberg, Karl (1965), Real and Abstract Analysis. A Modern Treatment of the Theory of Functions of a Real Variable, Graduate Texts in Mathematics 25, Berlin, Heidelberg, New York: Springer-Verlag, ISBN 978-0-387-90138-1, MR 0188387, Zbl 0137.03202
- Rudin, Walter (1974), Real and Complex Analysis, McGraw-Hill Series in Higher Mathematics (2nd ed.), New York, Düsseldorf, Johannesburg: McGraw-Hill Book Comp., ISBN 0-07-054233-3, MR 0344043, Zbl 0278.26001
This article incorporates material from Lebesgue decomposition theorem on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.