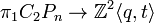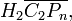Lawrence–Krammer representation
In mathematics the Lawrence–Krammer representation is a representation of the braid groups. It fits into a family of representations called the Lawrence representations. The 1st Lawrence representation is the Burau representation and the 2nd is the Lawrence–Krammer representation.
The Lawrence–Krammer representation is named after Ruth Lawrence and Daan Krammer.[1]
Definition
Consider the braid group 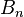 to be the mapping class group of a disc with n marked points
to be the mapping class group of a disc with n marked points  . The Lawrence–Krammer representation is defined as the action of
. The Lawrence–Krammer representation is defined as the action of 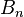 on the homology of a certain covering space of the configuration space
on the homology of a certain covering space of the configuration space 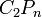 . Specifically,
. Specifically, 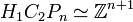 , and the subspace of
, and the subspace of 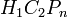 invariant under the action of
invariant under the action of 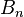 is primitive, free and of rank 2. Generators for this invariant subspace are denoted by
is primitive, free and of rank 2. Generators for this invariant subspace are denoted by 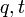 .
.
The covering space of 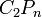 corresponding to the kernel of the projection map
corresponding to the kernel of the projection map
is called the Lawrence–Krammer cover and is denoted 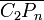 . Diffeomorphisms of
. Diffeomorphisms of act on
act on  , thus also on
, thus also on 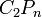 , moreover they lift uniquely to diffeomorphisms of
, moreover they lift uniquely to diffeomorphisms of 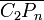 which restrict to identity on the co-dimension two boundary stratum (where both points are on the boundary circle). The action of
which restrict to identity on the co-dimension two boundary stratum (where both points are on the boundary circle). The action of 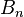 on
on
thought of as a
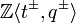 -module,
-module,
is the Lawrence–Krammer representation. 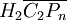 is known to be a free
is known to be a free 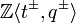 -module, of rank
-module, of rank  .
.
Matrices
Using Bigelow's conventions for the Lawrence–Krammer representation, generators for 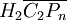 are denoted
are denoted 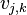 for
for 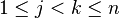 . Letting
. Letting 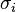 denote the standard Artin generators of the braid group, we get the expression:
denote the standard Artin generators of the braid group, we get the expression:
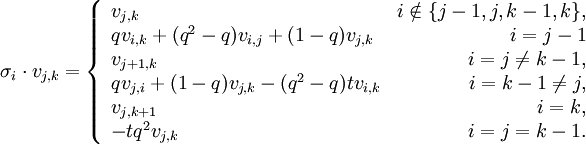
Faithfulness
Stephen Bigelow and Daan Krammer have independent proofs that the Lawrence–Krammer representation is faithful.
Geometry
The Lawrence–Krammer representation preserves a non-degenerate sesquilinear form which is known to be negative-definite Hermitian provided 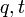 are specialized to suitable unit complex numbers (q near 1 and t near i). Thus the braid group is a subgroup of the unitary group of
are specialized to suitable unit complex numbers (q near 1 and t near i). Thus the braid group is a subgroup of the unitary group of 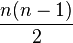 -square matrices. Recently it has been shown that the image of the Lawrence–Krammer representation is dense subgroup of the unitary group in this case.
-square matrices. Recently it has been shown that the image of the Lawrence–Krammer representation is dense subgroup of the unitary group in this case.
The sesquilinear form has the explicit description:
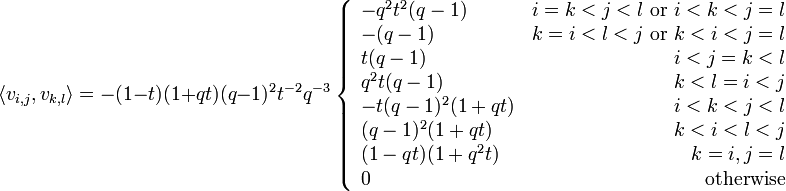
References
- S. Bigelow, Braid groups are linear, J. Amer. Math. Soc. 14 (2001), 471-486.
- S. Bigelow, The Lawrence–Krammer representation, Topology and geometry of manifolds, Proc. Sympos. Pure Math., 71 (2003)
- R. Budney, On the image of the Lawrence–Krammer representation, J Knot. Th. Ram. (2005)
- D. Krammer, Braid groups are linear, Ann. Math. 155 (2002), 131-156.
- L. Paoluzzi and L. Paris, A note on the Lawrence-Krammer-Bigelow representation, Alg. Geom. Topology 2 (2002), 499-518.
- ↑ Stephen Bigelow (2002). "The Lawrence–Krammer representation". v1. arXiv:math/0204057. Unsupported parameter(s) in cite arXiv (help)