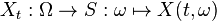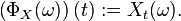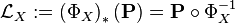Law (stochastic processes)

In mathematics, the law of a stochastic process is the measure that the process induces on the collection of functions from the index set into the state space. The law encodes a lot of information about the process; in the case of a random walk, for example, the law is the probability distribution of the possible trajectories of the walk.

Definition

Let (Ω, F, P) be a probability space, T some index set, and (S, Σ) a measurable space. Let X : T × Ω → S be a stochastic process (so the map

is a (F, Σ)-measurable function for each t ∈ T). Let S^T denote the collection of all functions from T into S. The process X (by way of currying) induces a function Φ_X : Ω → S^T, where

The law of the process X is then defined to be the pushforward measure

on S^T.

Example

• The law of standard Brownian motion is classical Wiener measure. (Indeed, many authors define Brownian motion to be a sample continuous process starting at the origin whose law is Wiener measure, and then proceed to derive the independence of increments and other properties from this definition; other authors prefer to work in the opposite direction.)

See also

• Finite-dimensional distribution
• stochastic process