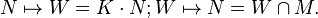Lattice (module)

In mathematics, in the field of ring theory, a lattice is a module over a ring which is embedded in a vector space over a field, giving an algebraic generalisation of the way a lattice group is embedded in a real vector space.

Formal definition

Let R be an integral domain with field of fractions K. An R-module M is a lattice in the K-vector space V if M is finitely generated, R-torsion-free (no non-zero element of M is annihilated by a regular element of R) and an R-submodule of V. It is full if V = K·M.^[1]

Pure sublattices

A submodule N of M which is again a lattice is an R-pure sublattice if M/N is R-torsionfree. There is a one-to-one correspondence between R-pure sublattices N of M and K-subspaces W of V given by^[2]

See also

• Lattice (group) for the case where M is a Z-module embedded in a vector space V over the field of real numbers R, and the Euclidean metric is used to describe the lattice structure

References

• Reiner, I. (2003). Maximal Orders. London Mathematical Society Monographs. New Series 28. Oxford University Press. ISBN 0-19-852673-3. Zbl 1024.16008.